Given, $$w=\frac{\sqrt{3}}{2}+\frac{i}{2}=e^{\frac{i \pi}{6}}$$

And $$\mathrm{P}=\left\{w^n: n=1,2,3, \ldots\right\}=e^{\text {in } \frac{\pi}{6}}, n=1,2,3, \ldots$$

Also given

$$\begin{aligned} & H_1=\left\{Z \in C: \operatorname{Re}(Z)>\frac{1}{2}\right\}, \\ & H_2=\left\{Z \in C: \operatorname{Re}(Z)<\frac{-1}{2}\right\} \end{aligned}$$

And $$\mathrm{Z}_1 \in \mathrm{P} \cap \mathrm{H}_1, \mathrm{Z}_2 \in \mathrm{P} \cap \mathrm{H}_2$$

Here, Possible values of P are $$e^{\frac{i \pi}{6}}, e^{\frac{i \pi}{3}}, e^{\frac{i \pi}{2}}, e^{\frac{i 2 \pi}{3}}, e^{\frac{i 5 \pi}{6}}, e^{i \pi}, e^{\frac{i 7 \pi}{6}}, e^{\frac{i 4 \pi}{6}}, e^{\frac{i 3 \pi}{2}}, e^{\frac{i 5 \pi}{3}}, e^{\frac{i 11 \pi}{6}}, e^{i 2 \pi}$$ And $$\mathrm{H}_1$$ and $$\mathrm{H}_2$$ are the set of all points at lies right side of $$x=\frac{1}{2}$$ and left side of $$x=-\frac{1}{2}$$ respectively

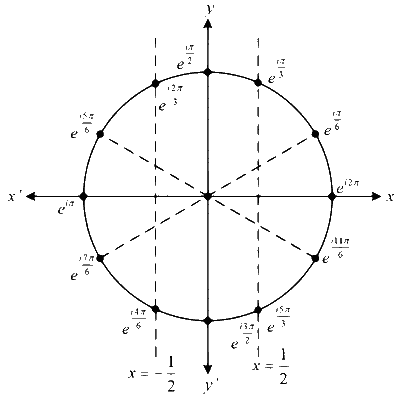
Here, $$\mathrm{Z}_1=e^{\frac{i \pi}{6}}$$ or $$e^{\frac{i 11 \pi}{6}}$$ or $$e^{i 2 \pi}$$ and $$\mathrm{Z}_2=e^{\frac{i 5 \pi}{6}} \text { or } e^{i \pi} \text { or } e^{\frac{i 7 \pi}{6}}$$

$$\text { Now, } \angle \mathrm{Z}_1 \mathrm{OZ}_2=\frac{2 \pi}{3} \text { or } \frac{5 \pi}{6} \text { or } \pi$$

Hints:

(i) $$\mathrm{H}_1$$ are the set of all points that lies right side of line $$x=\frac{1}{2}$$ and $$\mathrm{H}_2$$ are the set of all points that lies left of the line $$x=-\frac{1}{2}$$.

(ii) $$\mathrm{P}=\mathrm{W}^n$$ has 12 different roots lies on a unit circle and angle between two successive roots is $$\frac{\pi}{6}$$.