Given, $$S_1=\{z \in C:|z|<4\}$$ i.e. $$S_1$$ lies inside the circle of centre $$(0,0)$$ and radius 4.

Given, $$S_3=\{z \in C: \operatorname{Re}(z)>0\}$$ i.e. $$S_3$$ lies right side of the line $$x=0$$.

Also given $$S_2=\left\{z \in C: \operatorname{Im}\left(\frac{z-1+\sqrt{3} i}{1-\sqrt{3} i}\right)>0\right\}$$

Put $$z=x+i y$$ in $$\operatorname{Im}\left(\frac{z-1+\sqrt{3} i}{1-\sqrt{3} i}\right)>0$$

$$\begin{aligned} & \Rightarrow \operatorname{Im}\left(\frac{x-1+i(y+\sqrt{3})}{1-\sqrt{3} i}\right)>0 \\ & \Rightarrow \operatorname{Im}\left(\frac{(x-1)+i(y+\sqrt{3})}{1-\sqrt{3} i} \times \frac{1+\sqrt{3} i}{1+\sqrt{3} i}\right)>0 \\ & \Rightarrow \operatorname{Im}\left[\begin{array}{l} \frac{(x-1)-\sqrt{3}(y+\sqrt{3})}{4}+ \\ i\left(\frac{\sqrt{3}(x-1)+(y+\sqrt{3})}{4}\right) \end{array}\right]>0 \\ \end{aligned}$$

$$\begin{aligned} & \Rightarrow \quad \frac{\sqrt{3} x+y}{4}>0 \\ & \Rightarrow \sqrt{3} x+y>0 \end{aligned}$$

$$\text { So, } S_2 \text { lies above the line } \sqrt{3} x+y=0$$

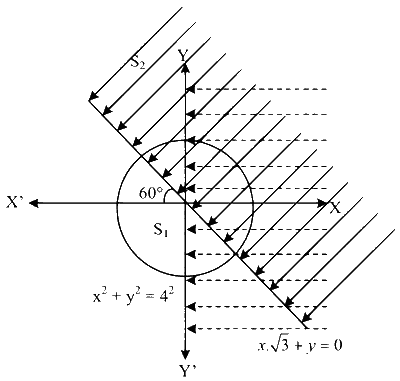
$$\text { Given, } S=S_1 \cap S_2 \cap S_3$$

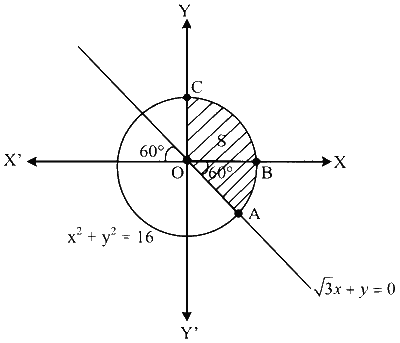
Here, $$\angle \mathrm{AOC}=\frac{\pi}{2}+\frac{\pi}{3}=\frac{5 \pi}{6}$$

Area of $$S=\frac{1}{2}\left(\frac{5 \pi}{6}\right) \cdot 4^2=\frac{20 \pi}{3}$$ Sq. Units

Hints:

(i) $$|z| < a$$ implies $$z$$ lies inside the circle of centre $$(0,0)$$ and radius $$a$$

(ii) $$\operatorname{Re}(z)>0$$ implies $$z$$ lies on the right side of the line $$x=0$$ i.e. $$y$$-axis.

(iii) Put $$z=x+i y$$ in the expression $$\operatorname{Im}\left(\frac{z-1+\sqrt{3} i}{1-\sqrt{3} i}\right)>0$$

(iv) If a circular arc $$A B$$ form $$\theta$$ angle at the centre of circle of radius R, then the area of this circular section is $$\frac{1}{2} \theta \cdot r^2$$