We know $$|1-3 i-z|=|z-(1-3 i)|$$ implies distance of $$z$$ from $$(1,-3)$$.

Let $$P=(1,-3)$$

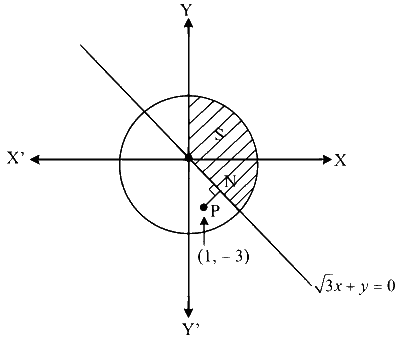
$$\min _{z \in \mathrm{S}}|1-3 i-z|=\mathrm{PN}$$

$$\begin{aligned} & \Rightarrow \min _{z \in S}|1-3 i-z|=\frac{|\sqrt{3} \cdot 1-3|}{\sqrt{(\sqrt{3})^2+1^2}} \\ & \Rightarrow \min _{z \in S}|1-3 i-z|=\frac{3-\sqrt{3}}{2} \end{aligned}$$

Hints:

(i) $$\left|z_1-z_2\right|$$ implies distance between $$z_1$$ and $$z_2$$

(ii) The minimum distance of a point $$\left(x_1, y_1\right)$$ from the line $$a x+b y+c=0$$ is $$\frac{\left|a x_1+b y_1+c\right|}{\sqrt{a^2+b^2}}$$.