Let a circle $$x^2+y^2+2 g x+2 f y+c=0$$ touches $$x$$-axis and have $y$-intercept of length $$2 \sqrt{7}$$.

$$\begin{aligned} & \therefore 2 \sqrt{g^2-c}=0 \text { and } 2 \sqrt{f^2-c}=2 \sqrt{7} \\ & \Rightarrow g^2=c \text { and } f^2-c=7 \\ & \Rightarrow c=g^2=f^2-7 \quad \text{... (i)} \end{aligned}$$

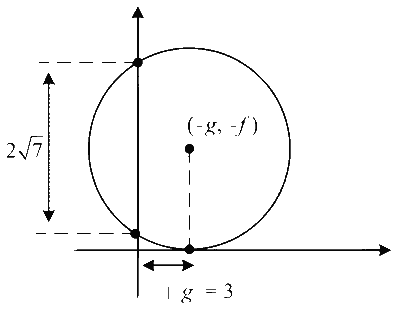
Given, the circle touches $$x$$-axis at a distance 3 unit from origin.

$$\begin{aligned} & \therefore|-g|=3 \\ & \Rightarrow g= \pm 3 \end{aligned}$$

Put $$g= \pm 3$$ in the equation

$$\Rightarrow c=9 \text { and } f= \pm 4$$

Hence, the possible equation of circles are

$$\begin{aligned} & x^2+y^2-6 x+8 y+9=0, \\ & x^2+y^2-6 x-8 y+9=0, \end{aligned}$$

$$\begin{aligned} & x^2+y^2+6 x+8 y+9=0 \text { and } x^2+y^2+6 x-8 y \\ & +9=0 \end{aligned}$$

Hints:

The length of X-intercept and Y-intercept of the circle $$x^2+y^2+2 g x+2 f y+c=0$$ are $$2 \sqrt{g^2-c}$$ and $$2 \sqrt{f^2-c}$$ respectively.