Given, a parabola $$y^2=16 x$$

Let $$\mathrm{F}\left(x_0, y_0\right)=\left(4 t^2, 8 t\right)$$

$$\Rightarrow \quad x_0=4 t^2, y_0=8 t$$

Equation of tangent at F is $$t y=x+4 t^2$$

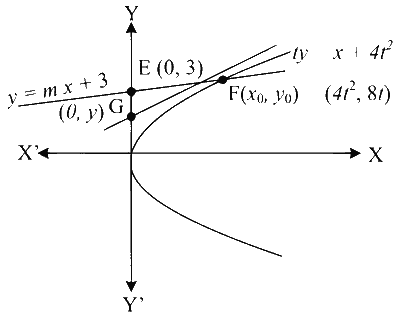
G is the point of intersection of tangent $$t y=x +4 t^2$$ and $$Y$$-axis

$$\therefore \mathrm{G}=(0,4 t)$$

Given, $$\mathrm{G}=\left(0, y_1\right)$$

$$\therefore \quad y_1=4 t$$

Let $$\Delta$$ be the area of $$\Delta$$ EGF

$$\begin{aligned} & \Rightarrow \quad \Delta=\frac{1}{2} 4 t^2 \cdot\left(3-y_1\right) \\ & \Rightarrow \quad \Delta=2 t^2(3-4 t) \\ & \Rightarrow \quad \frac{d \Delta}{d t}=12 t-24 t^2=0 \text { at } t=0, \frac{1}{2} \\ & \Rightarrow \frac{d^2 \Delta}{d t^2}=12-48 t<0 \text { at } t=\frac{1}{2} \end{aligned}$$

Hence, $$\Delta$$ is maximum at $$t=\frac{1}{2}$$

$$\therefore \quad \Delta_{\max }=\frac{1}{2}, y_0=8 t=4, y_1=4 t=2$$

Given, $$y=m x+3$$ intersect the parabola $$y^2=16 x$$ at $$\mathrm{F}\left(4 t^2, 8 t\right)$$

$$\therefore 8 t=4 m t^2+3$$

Put $$t=\frac{1}{2}$$

$$\begin{aligned} & \Rightarrow \quad 4=m+3 \\ & \Rightarrow m=1 \end{aligned}$$

Hints :

(i) $$\frac{d y}{d x}=0$$ at $$x=\alpha$$ and $$\frac{d^2 y}{d x^2}<0$$ at $$x=\alpha$$, then the function has point of local maxima at $$x=a$$.

(ii) The parametric point of the parabola $$y^2= 4 a x$$ is $$\left(a t^2, 2 a t\right)$$

(iii) The equation of tangent of parabola $$y^2=4 a x$$ at $$\left(a t^2, 2 a t\right)$$ is $$t y=x+a t^2$$.