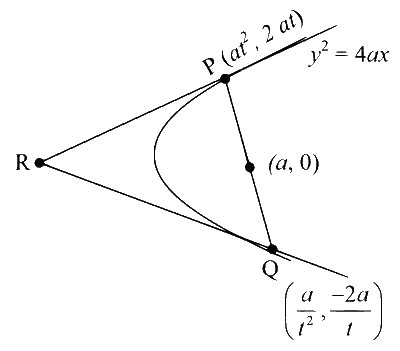
Given, PQ be a focal chord of the parabola $$y^2=4 a x$$

Let $$\mathrm{P}=\left(a t^2, 2 a t\right)$$ and $$\mathrm{Q}\left(\frac{a}{t^2},-\frac{2 a}{t}\right)$$

Equation of tangent at P is $$t y=x+a t^2\quad \text{... (i)}$$

Equation of tangent at Q is $$-\frac{y}{t}=x+\frac{a}{t^2}\quad \text{... (ii)}$$

Let $$R$$ is the point of intersection of tangents at $$P$$ and $$Q$$.

On solving Equation (i) and (ii)

$$\Rightarrow \mathrm{R}=\left(-a, a\left(t-\frac{1}{t}\right)\right)$$

Given, the tangents of parabola $$y^2=4 a x$$ at P and $$Q$$ meet at a point lying on the line $$y=2 x +a$$.

$$\therefore \mathrm{R}$$ must be lies on the line $$y=2 x+a$$

$$\begin{aligned} & \Rightarrow \quad a\left(t-\frac{1}{t}\right)=-2 a+a \\ & \Rightarrow \quad t-\frac{1}{t}=-1 \quad \text{... (iii)} \end{aligned}$$

Let the length of chord PQ is L

$$\begin{aligned} & \Rightarrow \mathrm{L}=\sqrt{\left(a t^2-\frac{a}{t^2}\right)^2+\left(2 a t+\frac{2 a}{t}\right)^2} \\ & \Rightarrow \mathrm{L}=a \sqrt{\left(t-\frac{1}{t}\right)^2\left(t+\frac{1}{t}\right)^2+4\left(t+\frac{1}{t}\right)^2} \\ & \Rightarrow \mathrm{L}=a \sqrt{\left(t-\frac{1}{t}\right)^2\left(\left(t-\frac{1}{t}\right)^2+4\right)+4\left(\left(t-\frac{1}{t}\right)^2+4\right)} \\ & \Rightarrow \mathrm{L}=a \sqrt{1 \cdot(1+4)+4 \cdot(1+4)} \\ & \Rightarrow \mathrm{L}=5 a \end{aligned}$$

Hints:

If $$P Q$$ is a focal chord of parabola $$y^2=4 a x$$, then $$\mathrm{P}=\left(a t^2, 2 a t\right)$$ and $$\mathrm{Q}=\left(\frac{a}{t^2}, \frac{-2 a}{t}\right)$$