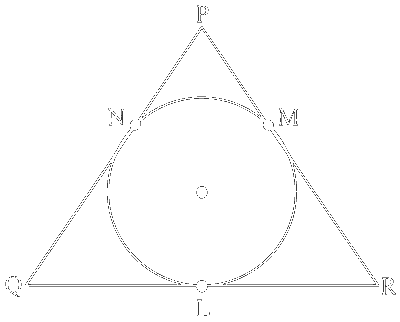
For the above circle PN and PM are its pair of tangents. So, its length are equal i.e. $$|\mathrm{PN}|=|\mathrm{PM}| \text {. }$$

Similarly $$|\mathrm{QL}|=|\mathrm{QN}|$$ and $$|\mathrm{RL}|=|\mathrm{RM}|$$

Let $$|\mathrm{PN}|=|\mathrm{PM}|=x,|\mathrm{QL}|=|\mathrm{QN}|=y$$ and $$|R L|=|R M|=z$$

Given $$|\mathrm{PN}|,|\mathrm{QL}|$$ and $$|\mathrm{RM}|$$ are consecutive even integer

$$\therefore \quad x=2 n, y=2 n+2 \text { and } z=2 n+4$$

Given, $$\cos P=\frac{1}{3}$$

$$\begin{aligned} & \Rightarrow \quad \frac{(4 n+4)^2+(4 n+2)^2-(4 n+6)^2}{2(4 n+4)(4 n+2)}=\frac{1}{3} \\ & \left(16 n^2+16+32 n\right)+\left(16 n^2+4+16 n\right) \\ & \Rightarrow \frac{-\left(16 n^2+36+48 n\right)}{32 n^2+48 n+16}=\frac{1}{3} \\ & \Rightarrow \quad 48 n^2-48=32 n^2+48 n+16 \\ & \Rightarrow \quad 16 n^2-48 n-64=0 \\ & \Rightarrow \quad n^2-3 n-4=0 \\ & \Rightarrow \quad n^2-4 n+n-4=0 \\ & \Rightarrow \quad(n-4)(n+1)=0 \\ & \Rightarrow \quad n=4 \\ \end{aligned}$$

$$\begin{aligned} & \text { Now }|P Q|=4 n+2=18,|Q R|=4 n+6=22 \\ & \text { and }|R P|=4 n+4=20 \end{aligned}$$

Hints :

(i) Recall cosine rule in a triangle $$\triangle \mathrm{ABC}$$,

$$\begin{aligned} & \cos \mathrm{A}=\frac{b^2+c^2-a^2}{2 b c}, \cos \mathrm{B}=\frac{c^2+a^2-b^2}{2 c a} \\ \text{and} \quad & \cos \mathrm{C}=\frac{a^2+b^2-c^2}{2 a b}\end{aligned}$$

(ii) Three consecutive even integers are $$2 n, 2 n +2,2 n+4$$ where $$n$$ is an integer.