$$\text { We know the graph of } y=x \sin x \text { is }$$

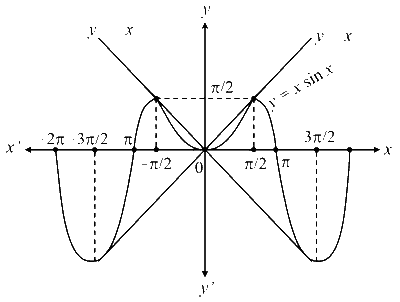
And the graph of $$y=\cos x$$ is

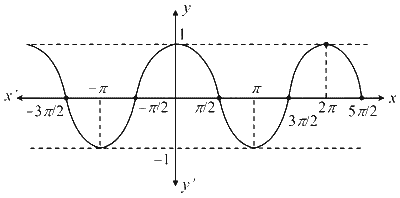
Now add the graph of $$y=x \sin x$$ and $$y=\cos x$$ and also draw the graph of $$y=x^2$$

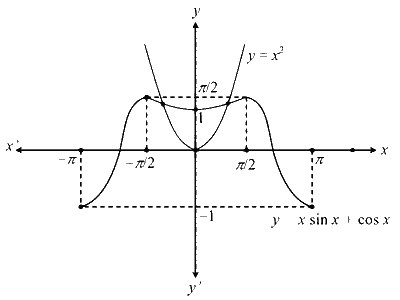
It is clear that the graph of $$y=x^2$$ and $$y=x \sin x +\cos x$$ intersect at two points

$$\therefore$$ The equation $$x^2=x \sin x+x$$ satisfy for two values of $$x$$.

Hints:

(i) Recall the graph of $$y=x \sin x, y=\cos x$$ and $$y=x^2$$.

(ii) Recall the method of addition of two graphs.

(iii) The number of point of intersection of graphs of $$y=f(x)$$ and $$y=g(x)$$ is equal to the number of solution of $$f(x)=g(x)$$