Given that $\overrightarrow{\mathrm{PR}} = 3 \hat{i} + \hat{j} - 2 \hat{k}$ and $\overrightarrow{\mathrm{SQ}} = \hat{i} - 3 \hat{j} - 4 \hat{k}$ are the diagonals of the parallelogram $PQRS$,

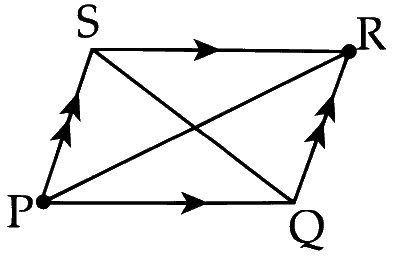
we have the following relationships:

$ \begin{aligned} \overrightarrow{\mathrm{PR}} &= \overrightarrow{\mathrm{PQ}} + \overrightarrow{\mathrm{QR}} \\ \overrightarrow{\mathrm{SQ}} &= \overrightarrow{\mathrm{PQ}} - \overrightarrow{\mathrm{PS}} \\ \end{aligned} $

Since $\overrightarrow{\mathrm{QR}} = \overrightarrow{\mathrm{PS}}$,

$ \overrightarrow{\mathrm{PQ}} = \frac{\overrightarrow{\mathrm{PR}} + \overrightarrow{\mathrm{SQ}}}{2} $

and

$ \overrightarrow{\mathrm{PS}} = \frac{\overrightarrow{\mathrm{PR}} - \overrightarrow{\mathrm{SQ}}}{2}. $

Substituting the values of $\overrightarrow{\mathrm{PR}}$ and $\overrightarrow{\mathrm{SQ}}$,

$ \begin{aligned} \overrightarrow{\mathrm{PQ}} &= \frac{(3 \hat{i} + \hat{j} - 2 \hat{k}) + (\hat{i} - 3 \hat{j} - 4 \hat{k})}{2} \\ &= \frac{4 \hat{i} - 2 \hat{j} - 6 \hat{k}}{2} \\ &= 2 \hat{i} - \hat{j} - 3 \hat{k}, \end{aligned} $

$ \begin{aligned} \overrightarrow{\mathrm{PS}} &= \frac{(3 \hat{i} + \hat{j} - 2 \hat{k}) - (\hat{i} - 3 \hat{j} - 4 \hat{k})}{2} \\ &= \frac{2 \hat{i} + 4 \hat{j} + 2 \hat{k}}{2} \\ &= \hat{i} + 2 \hat{j} + \hat{k}. \end{aligned} $

Given $\overrightarrow{\mathrm{PT}} = \hat{i} + 2 \hat{j} + 3 \hat{k}$,

To find the volume $V$ of the parallelepiped formed by $\overrightarrow{\mathrm{PT}}, \overrightarrow{\mathrm{PQ}},$ and $\overrightarrow{\mathrm{PS}}$, we calculate the determinant of the following matrix:

$ V = \left| \begin{array}{ccc} 1 & 2 & 3 \\ 2 & -1 & -3 \\ 1 & 2 & 1 \end{array} \right|. $

Calculating this determinant:

$ \begin{aligned} V &= 1(-1 \times 1 + 6) - 2(2 + 3) + 3(4 + 1) \\\\ &= 1 \times 5 - 2 \times 5 + 3 \times 5 \\\\ &= 5 - 10 + 15\\\\ &= 10. \end{aligned} $

Thus, the volume of the parallelepiped is 10 units.