Draw the graph of $$y=\sin x+\cos x$$ and $$y=|\cos x-\sin x|$$

$$\text { For } x \in\left[0, \frac{\pi}{2}\right]$$

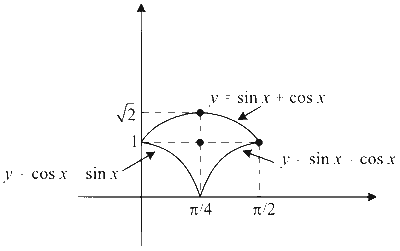
Let A be the area bounded by curves $$y=\sin x +\cos x$$ and $$y=|\cos x+\sin x|$$ for $$x \in\left[0, \frac{\pi}{2}\right]$$

$$\begin{aligned} \mathrm{A} & =2 \int_\limits0^{\frac{\pi}{4}}((\sin x+\cos x)-(\cos x-\sin x)) d x \\ \mathrm{~A} & =4 \int_\limits0^{\frac{\pi}{4}} \sin x d x \\ \Rightarrow \mathrm{A} & =4[-\cos x]_0^{\frac{\pi}{4}} \\ \Rightarrow \mathrm{A} & =4\left[\frac{-1}{\sqrt{2}}+1\right] \\ \Rightarrow \mathrm{A} & =2 \sqrt{2}(\sqrt{2}-1) \text { sq. units } \end{aligned}$$

Hints:

(i) the area bounded by curves $$y=f(x)$$ and $$y=g(x)$$ and the lines $$x=a$$ and $$x=b(b>a)$$ is $$\int_\limits a^b|f(x)-g(x)| d x$$

(ii) Recall the graph of $$y=\sin x+\cos x$$ and $$y=\cos x-\sin x$$

(iii) Recall the graphical transformation $$y=f (x)$$ in to $$y=|f(x)|$$.