Let $$a$$ rectangular sheet with sides $$15 a$$ and $$8 a$$ and four squares of side length $$b$$ removing from each corners of the rectangular sheet

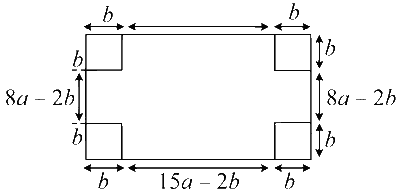
Given, the perimeter of rectangular sheet is constant.

$$\therefore 15 a+8 a=$$ Constant

$$\Rightarrow a$$ is constant

Let $$V$$ be the volume of open rectangular box

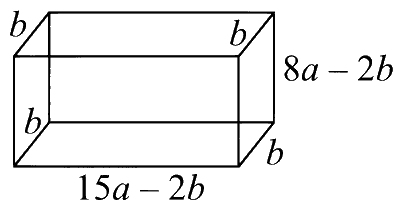
$$\begin{aligned} & \Rightarrow \quad \mathrm{V}=(15 a-2 b) b(8 a-2 b) \\ & \Rightarrow \quad \mathrm{V}=4 b^3-46 a b^2+120 a^2 b \\ & \Rightarrow \quad \frac{d \mathrm{~V}}{d b}=12 b^2-92 a b+120 a^2=0 \\ & \Rightarrow \quad \frac{d \mathrm{~V}}{d b}=4(3 b-5 a)(b-6 a)=0 \\ & \Rightarrow \quad b=\frac{5 a}{3}, 6 a \\ \end{aligned}$$

Now $$\frac{d^2 v}{d b^2}=24 b-92 a<0$$ at $$b=\frac{5 a}{3}$$

So, $$b=\frac{5 a}{3}$$ is the point of local maxima

Given, the area of removed squares is 100

$$\begin{aligned} & \therefore & 4 b^2 & =100 \\ & \Rightarrow & b^2 & =25 \\ & \Rightarrow & \left(\frac{5 a}{3}\right)^2 & =25 \\ & \Rightarrow & a & =3 \end{aligned}$$

Hence, the side length of the given rectangular sheet are $$15 a=45$$ and $$8 a=24$$.

Hints:

$$\Rightarrow$$ If $$x=x_0$$ is the point of local maxima of a function $$y=f(x)$$, then $$f^{\prime}\left(x_0\right)=0$$ and $$f^{\prime \prime}\left(x_0\right)<0$$