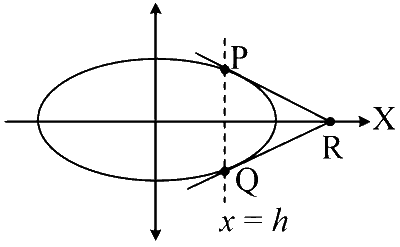
A vertical line passing through $$(h, 0)$$ is $$x=h$$ and this vertical line intersect the ellipse $$\frac{x^2}{4}+\frac{y^2}{3}=1$$ at P and Q.

Put $$x=h$$ in the ellipse $$\frac{x^2}{4}+\frac{y^2}{3}=1$$

$$\begin{aligned} & \Rightarrow \frac{h^2}{4}+\frac{y^2}{3}=1 \\ & \Rightarrow y= \pm \sqrt{3-\frac{3 h^2}{4}} \end{aligned}$$

So $$\mathrm{P}=\left(h, \sqrt{3-\frac{3 h^2}{4}}\right)$$ and $$\mathrm{Q}=\left(h,-\sqrt{3-\frac{3 h^2}{4}}\right)$$

Equation of tangent of ellipse $$\frac{x^2}{4}+\frac{y^2}{3}=1$$ at P is

$$\frac{h x}{4}+\frac{y}{3} \sqrt{3-\frac{3 h^2}{4}}=1 \quad \text{... (i)}$$

Equation of tangent of ellipse $$\frac{x^2}{4}+\frac{y^2}{3}=1$$ at Q is

$$\frac{h x}{4}-\frac{y}{3} \sqrt{3-\frac{3 h^2}{4}}=1 \quad \text{... (ii)}$$

Given, $$R$$ is the point of intersection of tangents at $$P$$ and at $$Q$$.

On solving the equations (i) and (ii)

$$\Rightarrow \quad \mathrm{R}=\left(\frac{8}{h}, 0\right)$$

Given, $$\Delta(h)=$$ Area of $$\Delta \mathrm{PQR}$$

$$\begin{aligned} \Rightarrow \quad \Delta(h) & =\frac{1}{2}\left(\frac{8}{h}-h\right) \cdot 2 \sqrt{3-\frac{3 h^2}{4}} \\ \Rightarrow \quad \Delta(h) & =\frac{\sqrt{3}}{2}\left(\frac{8}{h}-h\right) \sqrt{4-h^2} \\ \Rightarrow \quad \frac{d \Delta(h)}{d h}= & \frac{\sqrt{3}}{2}\left(\frac{-8}{h^2}-1\right) \sqrt{4-h^2} +\frac{\sqrt{3}}{2}\left(\frac{8}{h}-h\right) \cdot \frac{(-2 h)}{2 \sqrt{4-h^2}} \end{aligned}$$

$$\begin{aligned} \Rightarrow \quad \frac{d \Delta(h)}{d h}= & \frac{-\sqrt{3}}{2 \sqrt{4-h^2}} \\ & {\left[\left(\frac{8}{h^2}+1\right)\left(4-h^2\right)+\left(\frac{8}{h}-h\right) h\right] } \end{aligned}$$

$$\begin{aligned} & \Rightarrow \quad \frac{d \Delta(h)}{d h}=\frac{-\sqrt{3}}{2 \sqrt{4-h^2}}\left[\frac{32}{h^2}-8+4-\hbar^2+8-h^2\right] \\ & \Rightarrow \quad \frac{d \Delta(h)}{d h}=\frac{-\sqrt{3}}{2 \sqrt{4-h^2}}\left[-2 h^2+\frac{32}{h^2}+4\right] \\ & \Rightarrow \quad \frac{d \Delta(h)}{d h}=\frac{\sqrt{3}}{h^2 \sqrt{4-h^2}}\left[h^4-2 h^2-16\right] \\ & \Rightarrow \quad \frac{d \Delta(h)}{d h}=\frac{\sqrt{3}}{h^2 \sqrt{4-h^2}}\left[\left(h^2-1\right)^2-17\right] \end{aligned}$$

For, $$\frac{1}{2} \leq h \leq 1, \quad \frac{d \Delta(h)}{d h}<0$$

$$\therefore \quad \Delta(h)$$ is a decreasing function for $$x \in\left[\frac{1}{2}, 1\right]$$

$$\Rightarrow \Delta(1) \leq \Delta(h) \leq \Delta\left(\frac{1}{2}\right)$$

Given $$\quad \Delta_1=\max _{\frac{1}{2} \leq h \leq 1} \Delta(h)$$ and

$$\begin{aligned} \Delta_2 & =\min _{\frac{1}{2} \leq h \leq 1} \Delta(h) \\ \Rightarrow \quad \Delta_1 & =\Delta\left(\frac{1}{2}\right) \text { and } \Delta_2=\Delta(1) \\ \Rightarrow \quad \Delta_1 & =\frac{\sqrt{3}}{2}\left(16-\frac{1}{2}\right) \sqrt{4-\frac{1}{4}} \text { and } \\ \Delta_2 & =\frac{\sqrt{3}}{2}(8-1) \sqrt{4-1} \\ \Rightarrow \quad \Delta_1 & =\frac{\sqrt{3}}{2} \times \frac{31}{2} \times \frac{\sqrt{5} \cdot \sqrt{3}}{2} \text { and } \Delta_2=\frac{21}{2} \\ \Rightarrow \quad \frac{8 \Delta_1}{\sqrt{5}} & =93 \text { and } 8 \Delta_2=84 \end{aligned}$$

$$\Rightarrow \frac{8 \Delta_1}{\sqrt{5}}-8 \Delta_2=9$$

Hints:

(i) If $$f(x)$$ is a decreasing function in $$x \in[a, b]$$, then $$f(b) \leq f(x) \leq f(a)$$

(ii) If $$\left(x_1, y_1\right)$$ is a point on the curve $$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$$, then equation of tangent at $$\left(x_1, y_1\right)$$ is $$\frac{x x_1}{a^2}+\frac{y y_1}{b^2}=1$$.