JEE Advance - Mathematics (2012 - Paper 2 Offline - No. 8)
$$g\left( x \right) = \int\limits_1^x {\left( {{{2\left( {t - 1} \right)} \over {t + 1}} - In\,t} \right)f\left( t \right)dt} $$ for all $$x \in \left( {1,\,\infty } \right)$$.
Consider the statements:
$$P:$$ There exists some $$x \in R$$ such that $$f\left( x \right) + 2x = 2\left( {1 + {x^2}} \right)$$
$$Q:\,\,$$ There exists some $$x \in R$$ such that $$2\,f\left( x \right) + 1 = 2x\left( {1 + x} \right)$$
Then
Explanation
For statement $$P$$
$$\begin{aligned} & f(x)+2 x=2\left(1+x^2\right) \\ \Rightarrow & (1-x)^2 \sin ^2 x+x^2+2 x=2+2 x^2 \\ \Rightarrow & (1-x)^2 \sin ^2 x=x^2-2 x+1+1 \\ \Rightarrow & (1-x)^2 \sin ^2 x=(1-x)^2+1 \\ \Rightarrow & -(1-x)^2\left(1-\sin ^2 x\right)=1 \\ \Rightarrow & -\cos ^2 x=\frac{1}{(1-x)^2}>0 \\ \Rightarrow & \cos ^2 x<0 \end{aligned}$$
Here, no value of $$x$$ that satisfy the above equation.
$$\therefore$$ Statement P is false
For Statement Q
$$\begin{aligned} & 2 f(x)+1=2 x(1+x) \\ \Rightarrow \quad & 2(1-x)^2 \sin ^2 x+2 x^2+1=2 x+2 x^2 \\ \Rightarrow \quad & 2(x-1)^2 \sin ^2 x=2 x-1 \\ \Rightarrow \quad & \sin ^2 x=\frac{2 x-1}{2(x-1)^2} \\ \Rightarrow \quad & \sin ^2 x=\frac{1}{x-1}+\frac{1}{2(x-1)^2} \quad \text{... (i)} \end{aligned}$$
$$\begin{aligned} \text { Let } B(x) & =\frac{1}{x-1}+\frac{1}{2(x-1)^2} \\ \Rightarrow \quad B^{\prime}(x) & =\frac{-1}{(x-1)^2}-\frac{1}{(x-1)^3}=\frac{-x}{(x-1)^3} \text { and } \\ B^{\prime \prime}(x) & =\frac{2 x+1}{(x-1)^4} \end{aligned}$$
Hence, $$\mathrm{B}(x)$$ is increasing function on $$x \in(0,1)$$ and decreasing on $$x \in(-\infty, 0) \cup(1, \infty), \mathrm{B}^{\prime \prime}(x)=0$$ at $$x=-\frac{1}{2}$$ and $$\mathrm{B}^{\prime \prime}(x) \geq 0$$ for $$x \in \mathrm{R}-\left\{\frac{-1}{2}, 1\right\} \text {. }$$
Draw the graph of the $$y=\sin ^2 x$$ and $$y=\frac{1}{x+1}+\frac{1}{2(x-1)^2}$$
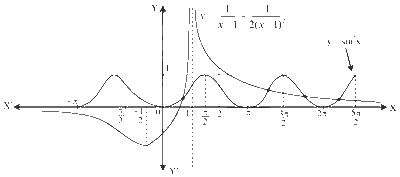
The graph of $$y=\sin ^2 x$$ and $$y=\frac{1}{x+1}+\frac{1}{2(x-1)^2}$$ intersect at some $$x$$.
Hence, statement $$Q$$ is true.
Comments (0)


