$$\begin{aligned} & \text { Given, } f(x)=|x|+\left|x^2-1\right| \\ & \Rightarrow f(x)=|x|+|x-1||x+1| \end{aligned}$$

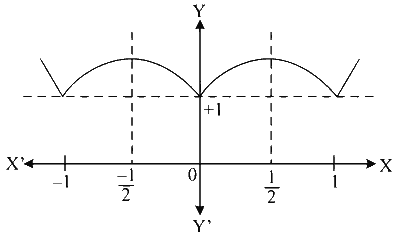
$$\begin{aligned} f(x) & =x^2+x-1, x \geq 1 \\ & =1-x^2+x, 0 \leq x < 1 \\ & =1-x^2-x,-1 < x < 0 \\ & =x^2-x-1, x \leq-1 \\ f^{\prime}(x) & =2 x+1 \quad(+v e) \\ & =1-2 x \quad x > \frac{1}{2}(+v e) \\ & =-2 x-1 \quad x > -\frac{1}{2}(-v e) ; x < \frac{-1}{2}(+v e) \\ & =2 x-1 \quad(-v e) \end{aligned}$$

From the figure, total number of points at which $$f$$ attains either a local maximum or a local minimum is 5.