JEE Advance - Mathematics (2011 - Paper 2 Offline - No. 5)
The straight line 2x - 3y = 1 divides the circular region $${x^2}\, + \,{y^2}\, \le \,6$$ into two parts.
If $$S = \left\{ {\left( {2,\,{3 \over 4}} \right),\,\left( {{5 \over 2},\,{3 \over 4}} \right),\,\left( {{1 \over 4} - \,{1 \over 4}} \right),\,\left( {{1 \over 8},\,{1 \over 4}} \right)} \right\}$$ then the number of points (s) in S lying inside the smaller part is
If $$S = \left\{ {\left( {2,\,{3 \over 4}} \right),\,\left( {{5 \over 2},\,{3 \over 4}} \right),\,\left( {{1 \over 4} - \,{1 \over 4}} \right),\,\left( {{1 \over 8},\,{1 \over 4}} \right)} \right\}$$ then the number of points (s) in S lying inside the smaller part is
Answer
2
Explanation
$$L:2x - 3y - 1$$
$$S:{x^2} + {y^2} - 6$$
If $${L_1} > 0$$ and $${S_1} < 0$$
The point lies in the smaller part. Therefore, $$\left( {2,{3 \over 4}} \right)$$ and $$\left( {{1 \over 4}, - {1 \over 4}} \right)$$ lie inside.
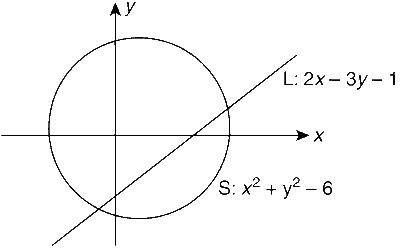
Comments (0)


