JEE Advance - Mathematics (2011 - Paper 1 Offline - No. 9)
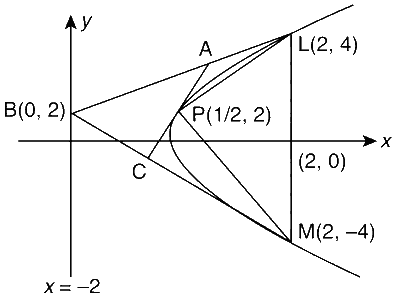
Consider the parabola $${y^2} = 8x$$. Let $${\Delta _1}$$ be the area of the triangle formed by the end points of its latus rectum and the point $$P\left( {{1 \over 2},2} \right)$$ on the parabola and $${\Delta _2}$$ be the area of the triangle formed by drawing tangents at $$P$$ and at the end points of the latus rectum. Then $${{{\Delta _1}} \over {{\Delta _2}}}$$ is
Answer
2
Explanation
The area of triangle formed by the three points on the parabola is twice the area of the triangle formed by the respective tangents. That is,
$$\Delta LPM = 2 \times $$ (Area of $$\Delta ABC$$)
$${y^2} = 8x = 4 \times 2 \times x$$
$${{\Delta LPM} \over {\Delta ABC}} = 2$$
$${{{\Delta _1}} \over {{\Delta _2}}} = 2$$
Comments (0)


