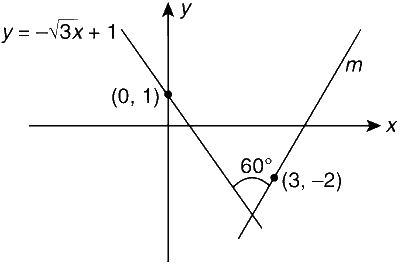
JEE Advance - Mathematics (2011 - Paper 1 Offline - No. 7)
A straight line $$L$$ through the point $$(3, -2)$$ is inclined at an angle $${60^ \circ }$$ to the line $$\sqrt {3x} + y = 1.$$ If $$L$$ also intersects the x-axis, then the equation of $$L$$ is
$$y + \sqrt {3x} + 2 - 3\sqrt 3 = 0$$
$$y - \sqrt {3x} + 2 + 3\sqrt 3 = 0$$
$$\sqrt {3y} - x + 3 + 2\sqrt 3 = 0$$
$$\sqrt {3y} + x - 3 + 2\sqrt 3 = 0$$
Explanation
We have $$\left| {{{m + \sqrt 3 } \over {1 - \sqrt 3 m}}} \right| = \sqrt 3 $$.
$$ \Rightarrow m + \sqrt 3 = \pm (\sqrt 3 - 3m)$$
$$ \Rightarrow 4m = 0 \Rightarrow m = 0$$
or $$2m = 2\sqrt 3 \Rightarrow m = \sqrt 3 $$
Therefore, the equation is
$$y + 2 = \sqrt 3 (x - 3)$$
$$ \Rightarrow \sqrt 3 x - y - (2 + 3\sqrt 3 ) = 0$$
Comments (0)


