JEE Advance - Mathematics (2011 - Paper 1 Offline - No. 11)
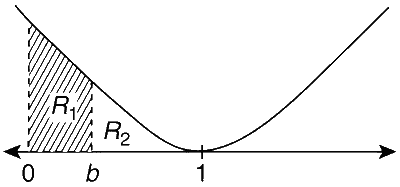
Let the straight line $$x=b$$ divide the area enclosed by
$$y = {\left( {1 - x} \right)^2},y = 0,$$ and $$x=0$$ into two parts $${R_1}\left( {0 \le x \le b} \right)$$ and
$${R_2}\left( {b \le x \le 1} \right)$$ such that $${R_1} - {R_2} = {1 \over 4}.$$ Then $$b$$ equals
$$y = {\left( {1 - x} \right)^2},y = 0,$$ and $$x=0$$ into two parts $${R_1}\left( {0 \le x \le b} \right)$$ and
$${R_2}\left( {b \le x \le 1} \right)$$ such that $${R_1} - {R_2} = {1 \over 4}.$$ Then $$b$$ equals
$${3 \over 4}$$
$${ 1\over 2}$$
$${1 \over 3}$$
$${1 \over 4}$$
Explanation
We can write the integral
$$\int\limits_0^b {{{(1 - x)}^2}dx - \int\limits_0^1 {{{(1 - x)}^2}dx = {1 \over 4}} } $$
$$ \Rightarrow \left. {{{{{(x - 1)}^3}} \over 3}} \right|_0^b - \left. {{{{{(x - 1)}^3}} \over 3}} \right|_b^1 = {1 \over 4}$$
$$ \Rightarrow {{{{(b - 1)}^3}} \over 3} + {1 \over 3} - \left( {0 - {{{{(b - 1)}^3}} \over 3}} \right) = {1 \over 4}$$
$$ \Rightarrow {{2{{(b - 1)}^3}} \over 3} = - {1 \over {12}} \Rightarrow {(b - 1)^3} = - {1 \over 8} \Rightarrow b = {1 \over 2}$$
Comments (0)


