JEE Advance - Mathematics (2010 - Paper 2 Offline - No. 9)
The orthocentre of the triangle $$PAB$$ is
$$\left( {5,{8 \over 7}} \right)$$
$$\left( {{7 \over 5},{{25} \over 8}} \right)$$
$$\left( {{11 \over 5},{{8} \over 5}} \right)$$
$$\left( {{8 \over 25},{{7} \over 5}} \right)$$
Explanation
Equation of AB is
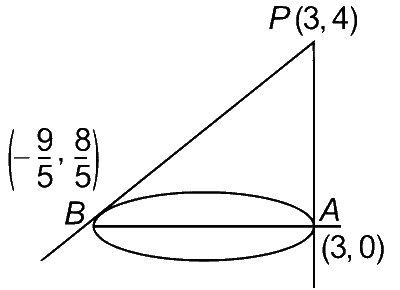
$$y - 0 = {{{8 \over 5}} \over { - {9 \over 5} - 3}}(x - 3) = {8 \over { - 24}}(x - 3)$$
$$ \Rightarrow y = - {1 \over 3}(x - 3)$$
$$ \Rightarrow x + 3y = 3$$ ...... (i)
Equation of the straight line perpendicular to AB through P is $$3x - y = 5$$.
Equation of PA is $$x - 3 = 0$$.
The equation of straight line perpendicular to PA through $$B\left( {{{ - 9} \over 5},{8 \over 5}} \right)$$ is $$y = {8 \over 5}$$.
Hence, the orthocentre is $$\left( {{{11} \over 5},{8 \over 5}} \right)$$.
Comments (0)


