Let $$\theta = {\pi \over {2k}}$$

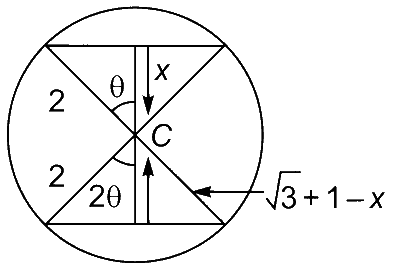
$$\cos \theta = {x \over 2}$$

$$ \Rightarrow \cos 2\theta = {{\sqrt 3 + 1 - x} \over 2}$$

$$ \Rightarrow 2{\cos ^2}\theta - 1 = {{\sqrt 3 + 1 - x} \over 2}$$

$$ \Rightarrow 2\left( {{{{x^2}} \over 4}} \right) - 1 = {{\sqrt 3 + 1 - x} \over 2}$$

$$ \Rightarrow {x^2} + x - 3 - \sqrt 3 = 0$$

$$ \Rightarrow x = {{ - 1 \pm \sqrt {1 + 12 + 4\sqrt 3 } } \over 2}$$

$$ = {{ - 1 \pm \sqrt {13 + 4\sqrt 3 } } \over 2}$$

$$ = {{ - 1 + 2\sqrt 3 + 1} \over 2} = \sqrt 3 $$

$$\therefore$$ $$\cos \theta = {{\sqrt 3 } \over 2} \Rightarrow \theta = {\pi \over 6}$$

$$\therefore$$ Required angle $$ = {\pi \over k} = 2\theta = {\pi \over 3}$$

$$ \Rightarrow k = 3$$