JEE Advance - Mathematics (2010 - Paper 2 Offline - No. 4)
If the distance of the point $$P(1, -2, 1)$$ from the plane $$x+2y-2z$$$$\, = \alpha ,$$ where $$\alpha > 0,$$ is $$5,$$ then the foot of the perpendicular from $$P$$ to the planes is
$$\left( {{8 \over 3},{4 \over 3}, - {7 \over 3}} \right)$$
$$\left( {{4 \over 3},-{4 \over 3}, {1 \over 3}} \right)$$
$$\left( {{1 \over 3},{2 \over 3}, {10 \over 3}} \right)$$
$$\left( {{2 \over 3},-{1 \over 3}, {5 \over 3}} \right)$$
Explanation
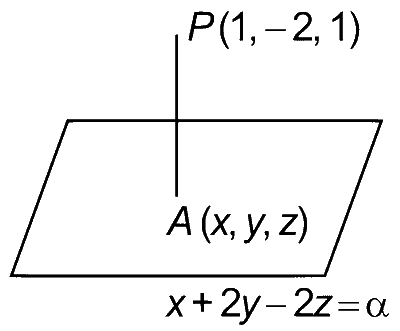
Distance of point P from plane = 5
$$\therefore$$ $$5 = \left| {{{1 - 4 - 2 - \alpha } \over 3}} \right|$$
$$\alpha = 10$$
Foot of perpendicular
$${{x - 1} \over 1} = {{y + 2} \over 2} = {{z - 1} \over { - 2}} = {5 \over 3}$$
$$ \Rightarrow x = {8 \over 3},y = {4 \over 3},z = - {7 \over 3}$$
Thus, the foot of the perpendicular is
$$A\left( {{8 \over 3},{4 \over 3}, - {7 \over 3}} \right)$$
Comments (0)


