JEE Advance - Mathematics (2010 - Paper 2 Offline - No. 19)
Two adjacent sides of a parallelogram $$ABCD$$ are given by
$$\overrightarrow {AB} = 2\widehat i + 10\widehat j + 11\widehat k$$ and $$\,\overrightarrow {AD} = -\widehat i + 2\widehat j + 2\widehat k$$
The side $$AD$$ is rotated by an acute angle $$\alpha $$ in the plane of the parallelogram so that $$AD$$ becomes $$AD'.$$ If $$AD'$$ makes a right angle with the side $$AB,$$ then the cosine of the angle $$\alpha $$ is given by
$$\overrightarrow {AB} = 2\widehat i + 10\widehat j + 11\widehat k$$ and $$\,\overrightarrow {AD} = -\widehat i + 2\widehat j + 2\widehat k$$
The side $$AD$$ is rotated by an acute angle $$\alpha $$ in the plane of the parallelogram so that $$AD$$ becomes $$AD'.$$ If $$AD'$$ makes a right angle with the side $$AB,$$ then the cosine of the angle $$\alpha $$ is given by
$${{8 \over 9}}$$
$${{{\sqrt {17} } \over 9}}$$
$${{1 \over 9}}$$
$${{{4\sqrt 5 } \over 9}}$$
Explanation
$$\overrightarrow {AB} = 2\widehat i + 10\widehat j + 11\widehat k$$
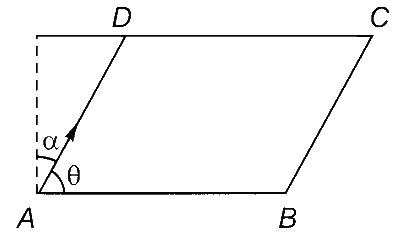
$$\overrightarrow {AD} = - \widehat i + 2\widehat j + 2\widehat k$$
Angle '$$\theta$$' between $$\overrightarrow {AB} $$ and $$\overrightarrow {AD} $$ is
$$\cos (\theta ) = \left| {{{\overrightarrow {AB} \,.\,\overrightarrow {AD} } \over {\left| {\overrightarrow {AB} } \right|\left| {\overrightarrow {AD} } \right|}}} \right|$$
$$ = \left| {{{ - 2 + 20 + 22} \over {(15)(3)}}} \right| = {8 \over 9}$$
$$ \Rightarrow \sin (\theta ) = {{\sqrt {17} } \over 9}$$
Since, $$\alpha + \theta = 90^\circ $$
$$\therefore$$ $$\cos (\alpha ) = \cos (90^\circ - \theta )$$
$$ = \sin (\theta ) = {{\sqrt {17} } \over 9}$$
Comments (0)


