JEE Advance - Mathematics (2010 - Paper 2 Offline - No. 18)
A signal which can be green or red with probability $${4 \over 5}$$ and $${1 \over 5}$$ respectively, is received by station A and then transmitted to station $$B$$. The probability of each station receving the signal correctly is $${3 \over 4}$$. If the signal received at atation $$B$$ is green, then the probability that the original signal was green is
$${3 \over 5}$$
$${6 \over 7}$$
$${20 \over 23}$$
$${9 \over 20}$$
Explanation
From the tree-diagram it follows that
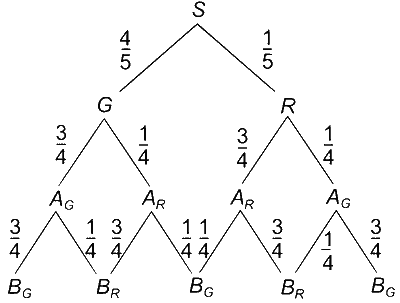
$$P({B_G}) = {{46} \over {80}}$$
$$P({B_G}|G) = {{10} \over {16}} = {5 \over 8}$$
$$\therefore$$ $$P({B_G} \cap G) = {5 \over 8} \times {4 \over 5} = {1 \over 2}$$
$$P(G|{B_G}) = {{{1 \over 2}} \over {P({B_G})}} = {1 \over 2} \times {{80} \over {46}} = {{20} \over {23}}$$
Comments (0)


