JEE Advance - Mathematics (2010 - Paper 2 Offline - No. 15)
Consider the polynomial
$$f\left( x \right) = 1 + 2x + 3{x^2} + 4{x^3}.$$
Let $$s$$ be the sum of all distinct real roots of $$f(x)$$ and let $$t = \left| s \right|.$$
The area bounded by the curve $$y=f(x)$$ and the lines $$x=0,$$ $$y=0$$ and $$x=t,$$ lies in the interval
$$\left( {{3 \over 4},3} \right)$$
$$\left( {{{21} \over {64}},{{11} \over {16}}} \right)$$
$$\left( {9,10} \right)$$
$$\left( {0,{{21} \over {64}}} \right)$$
Explanation
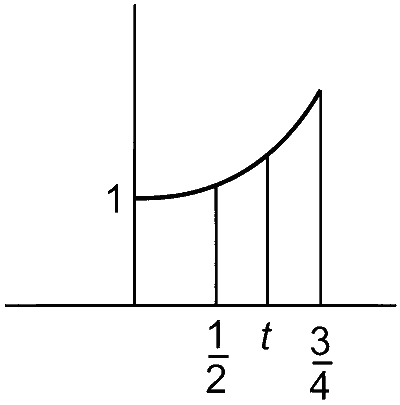
$$\int\limits_0^{1/2} {f(x)dx < \int\limits_0^t {f(x)dx < \int\limits_0^{3/4} {f(x)dx} } } $$
Now, $$\int\limits_{}^{} {f(x)dx} $$
$$ = \int\limits_{}^{} {(1 + 2x + 3{x^2} + 4{x^3})dx} $$
$$ = x + {x^2} + {x^3} + {x^4}$$
$$ \Rightarrow \int\limits_0^{1/2} {f(x)dx = {{15} \over {16}} > {3 \over 4}} $$
$$\int\limits_0^{3/4} {f(x)dx = {{530} \over {256}} < 3} $$
Comments (0)


