JEE Advance - Mathematics (2010 - Paper 1 Offline - No. 8)
Let $$A$$ and $$B$$ be two distinct points on the parabola $${y^2} = 4x$$. If the axis of the parabola touches a circle of radius $$r$$ having $$AB$$ as its diameter, then the slope of the line joining $$A$$ and $$B$$ can be
$$ - {1 \over r}$$
$$ {1 \over r}$$
$$ {2 \over r}$$
$$ - {2 \over r}$$
Explanation
Let A $$\equiv$$ (t$$_1^2$$, 2t1) and B $$\equiv$$ (t$$_2^2$$, 2t2)
The centre of the circle = $$\left( {{{t_1^2 + t_2^2} \over 2},{t_1} + {t_2}} \right)$$
As the circle touches the x-axis thus $${t_1} + {t_2} = \pm \,r$$
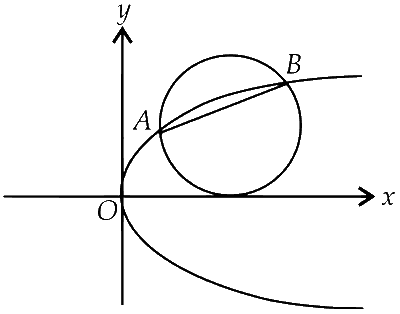
Slope of $$AB = {2 \over {{t_1} + {t_2}}} = \pm \,{2 \over r}$$
Comments (0)


