Sign In

JEE Advance - Mathematics (2010 - Paper 1 Offline - No. 5)

Let $${{z_1}}$$ and $${{z_2}}$$ be two distinct complex number and let z =( 1 - t)$${{z_1}}$$ + t$${{z_2}}$$ for some real number t with 0 < t < 1. IfArg (w) denote the principal argument of a non-zero complex number w, then
$$\left| {z - {z_1}} \right| + \left| {z - {z_2}} \right| = \left| {{z_1} - {z_2}} \right|$$
Arg $$(z - {z_1})$$ = Arg$$(z - {z_2})$$
$$\left| {\matrix{ {z - {z_1}} & {\overline z - {{\overline z }_1}} \cr {{z_2} - {z_1}} & {{{\overline z }_2} - {{\overline z }_1}} \cr } } \right|$$ = 0
Arg $$(z - {z_1})$$ = Arg$$({z_2} - {z_1})$$

Explanation

Given, $$z = {{(1 - t){z_1} + t\,{z_2}} \over {(1 - t) + t}}$$

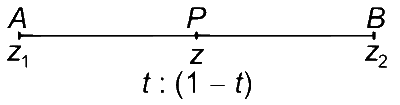
IIT-JEE 2010 Paper 1 Offline Mathematics - Complex Numbers Question 50 English Explanation

Clearly, z divides z1 and z2 in the ratio of t : (1 $$-$$ t), 0 < t < 1

$$\Rightarrow$$ AP + BP = AB

i.e., $$|z - {z_1}| + |z - {z_2}| = |{z_1} - {z_2}|$$

$$\Rightarrow$$ Option (a) is true.

and $$\arg (z - {z_1}) = \arg ({z_2} - z) = \arg ({z_2} - {z_1})$$

$$\Rightarrow$$ (b) is false and (d) is true.

Also, $$\arg (z - {z_1}) = \arg ({z_2} - {z_1})$$

$$ \Rightarrow \arg \left( {{{z - {z_1}} \over {{z_2} - {z_1}}}} \right) = 0$$

$$\therefore$$ $${{z - {z_1}} \over {{z_2} - {z_1}}}$$ is purely real.

$$ \Rightarrow {{z - {z_1}} \over {{z_2} - {z_1}}} = {{\overline z - {{\overline z }_1}} \over {{{\overline z }_2} - {{\overline z }_1}}}$$

or, $$\left| {\matrix{ {z - {z_1}} & {\overline z - {{\overline z }_1}} \cr {{z_2} - {z_1}} & {{{\overline z }_2} - {{\overline z }_1}} \cr } } \right| = 0$$

$$\therefore$$ Option (c) is correct.

Hence, (a, c, d) is the correct option.

Comments (0)

Advertisement