Sign In

JEE Advance - Mathematics (2010 - Paper 1 Offline - No. 25)

Let $z_1$ and $z_2$ be two distinct complex numbers let $z=(1-t) z_1+t z_2$ for some real number t with $0 < t < 1$.

If $\operatorname{Arg}(w)$ denotes the principal argument of a nonzero complex number $w$, then :

$\left|z-z_1\right|+\left|z-z_2\right|=\left|z_1-z_2\right|$
$\operatorname{Arg}\left(z-z_1\right)=\operatorname{Arg}\left(z-z_2\right)$
$\left|\begin{array}{cc}z-z_1 & \bar{z}-\bar{z}_1 \\ z_2-z_1 & \bar{z}_2-\bar{z}_1\end{array}\right|=0$
$\operatorname{Arg}\left(z-z_1\right)=\operatorname{Arg}\left(z_2-z_1\right)$

Explanation

$$ \begin{aligned} & \text { Given, } z=(1-t) z_1+t z_2 \\\\ & \Rightarrow \frac{z-z_1}{z_2-z_1}=t \\\\ & \Rightarrow \arg \left(\frac{z-z_1}{z_2-z_1}\right) = 0 .......(i) \end{aligned} $$

$\begin{aligned} \Rightarrow \arg \left(z-z_1\right) & =\arg \left(z_2-z_1\right) \\\\ \frac{z-z_1}{z_2-z_1} & =\frac{\bar{z}-\bar{z}_1}{\bar{z}_2-\bar{z}_1} \\\\ \left|\begin{array}{cc}z-z_1 & \bar{z}-\bar{z}_1 \\ z_2-z_1 & \bar{z}_2-\bar{z}_1\end{array}\right| & =0\end{aligned}$

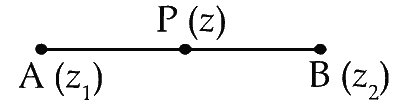
IIT-JEE 2010 Paper 1 Offline Mathematics - Complex Numbers Question 1 English Explanation

$\begin{gathered}\mathrm{AP}+\mathrm{PB}=\mathrm{AB} \\\\ \Rightarrow\left|z-z_1\right|+\left|z-z_2\right|=\left|z_1-z_2\right|\end{gathered}$

Comments (0)

Advertisement