JEE Advance - Mathematics (2010 - Paper 1 Offline - No. 2)
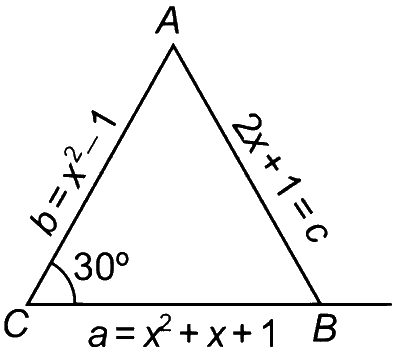
Let $$ABC$$ be a triangle such that $$\angle ACB = {\pi \over 6}$$ and let $$a, b$$ and $$c$$ denote the lengths of the sides opposite to $$A$$, $$B$$ and $$C$$ respectively. The value(s) of $$x$$ for which $$a = {x^2} + x + 1,\,\,\,b = {x^2} - 1\,\,\,$$ and $$c = 2x + 1$$ is (are)
$$ - \left( {2 + \sqrt 3 } \right)$$
$${1 + \sqrt 3 }$$
$${2 + \sqrt 3 }$$
$${4 \sqrt 3 }$$
Explanation
Using, $$\cos C = {{{a^2} + {b^2} - {c^2}} \over {2ab}}$$
$$ \Rightarrow {{\sqrt 3 } \over 2} = {{{{({x^2} + x + 1)}^2} + {{({x^2} - 1)}^2} - {{(2x + 1)}^2}} \over {2({x^2} + x + 1)({x^2} - 1)}}$$
$$ \Rightarrow (x + 2)(x + 1)(x - 1)x + {({x^2} - 1)^2} = \sqrt 3 ({x^2} + x + 1)({x^2} - 1)$$
$$ \Rightarrow {x^2} + 2x + ({x^2} - 1) = \sqrt 3 ({x^2} + x + 1)$$
$$ \Rightarrow (2 - \sqrt 3 ){x^2} + (2 - \sqrt 3 )x - (\sqrt 3 + 1) = 0$$
$$ \Rightarrow x = - (2 + \sqrt 3 )$$ and $$x = 1 + \sqrt 3 $$
But, $$x = - (2 + \sqrt 3 ) \Rightarrow c$$ is negative.
$$\therefore$$ $$x = 1 + \sqrt 3 $$ is the only solution.
Hence, (b) is the correct option.
Comments (0)


