JEE Advance - Mathematics (2010 - Paper 1 Offline - No. 19)
Let $$P,Q,R$$ and $$S$$ be the points on the plane with position vectors $${ - 2\widehat i - \widehat j,4\widehat i,3\widehat i + 3\widehat j}$$ and $${ - 3\widehat i + 2\widehat j}$$ respectively. The quadrilateral $$PQRS$$ must be a
parallelogram, which is neither a rhombus nor a rectangle
square
rectangle, but not a square
rhombus, but not a square
Explanation
We have $$PS = \sqrt {{1^2} + {3^2}} = \sqrt {10} $$
$$SR = \sqrt {{6^2} + {1^2}} = \sqrt {37} $$, $$RQ = \sqrt {{1^2} + {3^2}} = \sqrt {10} $$
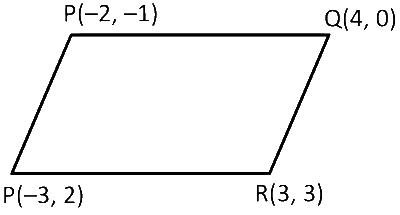
$$QP = \sqrt {{6^2} + {1^2}} = \sqrt {37} $$
Then PQRS is a parallelogram. It can be a rectangle, so let's check the product of slopes of PS and SR
$$({m_{PS}})\,.\,({m_{SR}}) = {3 \over { - 1}} \times {1 \over 6} = - {1 \over 2} \ne - 1$$
Thus PS and SR are not perpendicular. So, it's not a rectangle.
Also, $${m_{PR}}\,.\,{m_{QS}} = {4 \over 5} \times {2 \over { - 7}} = - {8 \over {35}} \ne - 1$$
Thus, PR and QS are also not perpendicular. So it's not a rhombus either.
Comments (0)


