JEE Advance - Mathematics (2009 - Paper 2 Offline - No. 15)
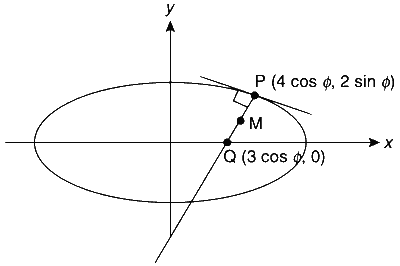
The normal at a point $$P$$ on the ellipse $${x^2} + 4{y^2} = 16$$ meets the $$x$$- axis $$Q$$. If $$M$$ is the mid point of the line segment $$PQ$$, then the locus of $$M$$ intersects the latus rectums of the given ellipse at the points
$$\left( { \pm {{3\sqrt 5 } \over 2},\, \pm {2 \over 7}} \right)$$
$$\left( { \pm {{3\sqrt 5 } \over 2},\, \pm \sqrt {{{19} \over 4}} } \right)$$
$$\left( { \pm 2\sqrt 3 , \pm {1 \over 7}} \right)$$
$$\left( { \pm 2\sqrt 3 , \pm {{4\sqrt 3 } \over 7}} \right)$$
Explanation
The normal is
$$4x\sec \phi - 2y\cos ec\phi = 12$$
Now, the points Q and M are given by
$$Q \equiv (3\cos \phi ,0)$$
$$M \equiv (\alpha ,\beta )$$
Therefore, $$\alpha = {{3\cos \phi + 4\cos \phi } \over 2} = {7 \over 2}\cos \phi \Rightarrow \cos \phi = {2 \over 7}\alpha $$
and $$\beta = \sin \phi ;{\cos ^2}\phi + {\sin ^2}\phi = 1$$.
Therefore, $${4 \over {49}}{\alpha ^2} + {\beta ^2} = 1 \Rightarrow {4 \over {49}}{x^2} + {y^2} = 1$$
Hence, the rectum is $$x = \pm 2\sqrt 3 $$.
Hence,
$${{48} \over {49}} + {y^2} = 1 \Rightarrow y = \pm {1 \over 7}$$
$$\left( { \pm 2\sqrt 3 , \pm {1 \over 7}} \right)$$
Hence, the locus of M intersects the latus rectum of the given ellipse at the points
Comments (0)


