JEE Advance - Mathematics Hindi (2025 - Paper 2 Online - No. 7)
मान लीजिए कि $P\left(x_1, y_1\right)$ और $Q\left(x_2, y_2\right)$, दीर्घवृत्त (ellipse)
$$ \frac{x^2}{9}+\frac{y^2}{4}=1 $$
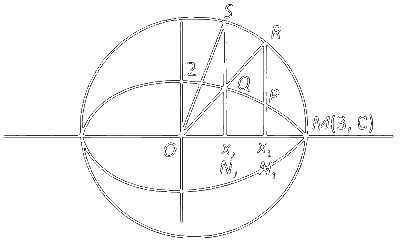
पर दो ऐसे भिन्न बिंदु हैं, कि $y_1>0$ और $y_2>0$ हैं। मान लीजिए कि $C$, वृत्त (circle) $x^2+y^2=9$ को दर्शाता है, और $M$, बिंदु $(3,0)$ है। मान लीजिए कि रेखा (line) $x=x_1$, वृत्त $C$ को $R$ पर प्रतिच्छेदित (intersect) करती है, और रेखा $x=x_2$, वृत्त $C$ को $S$ पर प्रतिच्छेदित करती है, जहाँ $R$ तथा $S$ के $y$-निर्देशांक ( $y$-coordinates) धनात्मक (positive) हैं।
मान लीजिए कि $\angle R O M=\frac{\pi}{6}$ और $\angle S O M=\frac{\pi}{3}$ हैं, जहाँ $O$ मूलबिंदु (origin) $(0,0)$ को दर्शाता है। मान लीजिए कि $|X Y|$, रेखाखंड (line segment) $X Y$ की लंबाई को दर्शाता है।
तब निम्नलिखित कथनों में से कौन सा (से) सत्य है (हैं) ?
Explanation
$\begin{aligned} & \mathrm{P} \equiv\left(3 \cos 30^{\circ}, 2 \sin 30^{\circ}\right) \equiv\left(\frac{3 \sqrt{3}}{2}, 1\right) \\ & \mathrm{Q} \equiv\left(3 \cos 60^{\circ}, 2 \sin 60^{\circ}\right) \equiv\left(\frac{3}{2}, \sqrt{3}\right) \\ & \mathrm{R}\left(\frac{3 \sqrt{3}}{2}, \frac{3}{2}\right), \mathrm{S}\left(\frac{3}{2}, \frac{3 \sqrt{3}}{2}\right)\end{aligned}$
$\mathrm{PQ}$ की प्रवणता (स्लोप) $=\mathrm{m}_{\mathrm{PQ}}=\frac{\sqrt{3}-1}{\frac{3}{2}-\frac{3 \sqrt{3}}{2}}=-\frac{2}{3}$
रेखा $PQ$ का समीकरण
$$ y-\sqrt{3}=-\frac{2}{3}\left(x-\frac{3}{2}\right) $$
$\Rightarrow 2 x+3 y=3(\sqrt{3}+1) \quad$ विकल्प (A) सही है
अब
यदि $\mathrm{N}_2=\left(\mathrm{x}_2, 0\right)=\left(\frac{3}{2}, 0\right)$
$\left|\mathrm{N}_2 \mathrm{Q}\right|=\sqrt{3}$ तथा $\left|\mathrm{N}_2 \mathrm{~S}\right|=\frac{3 \sqrt{3}}{2}$
$\Rightarrow 3\left|\mathrm{~N}_2 \mathrm{Q}\right|=2\left|\mathrm{~N}_2 \mathrm{~S}\right| \quad$ विकल्प (C) सही है
अब, यदि $\mathrm{N}_1=\left(\mathrm{x}_1, 0\right) \Rightarrow \mathrm{N}_1=\left(\frac{3 \sqrt{3}}{2}, 0\right)$
$\Rightarrow\left|\mathrm{N}_1 \mathrm{P}\right|=1,\left|\mathrm{~N}_1 \mathrm{R}\right|=\frac{3}{2} \quad$ विकल्प (D) गलत है
Comments (0)


