JEE Advance - Chemistry (2025 - Paper 2 Online - No. 12)
Consider a reaction $A+R \rightarrow$ Product. The rate of this reaction is measured to be $k[A][R]$. At the start of the reaction, the concentration of $R,[R]_0$, is 10-times the concentration of $A,[A]_0$. The reaction can be considered to be a pseudo first order reaction with assumption that $k[R]=k^{\prime}$ is constant. Due to this assumption, the relative error (in %) in the rate when this reaction is $40 \%$ complete, is ___________.
[ $k$ and $k^{\prime}$ represent corresponding rate constants]
Explanation
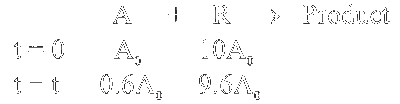$\begin{aligned} & \text { Rate }=k[\mathrm{~A}][\mathrm{R}] \\\\ & \operatorname{Rate}_1=k\left(0.6 \mathrm{~A}_0\right) \times 9.6 \mathrm{~A}_0\end{aligned}$
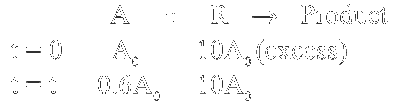$\begin{aligned} & \text { Rate }=\mathrm{k}^{\prime}[\mathrm{A}], \mathrm{k}^{\prime}=\mathrm{k}[\mathrm{R}] \end{aligned}$
The relative error between the actual rate and the pseudo-first order rate is computed by:
$ \text{Relative Error (%)} = \frac{\text{Rate}_2 - \text{Rate}_1}{\text{Rate}_1} \times 100 $
Plugging the calculations:
$ \text{Relative Error (%)} = \frac{(0.6 \times 10 - 0.6 \times 9.6)}{0.6 \times 9.6} \times 100 = 4.1666\% $
Comments (0)
