JEE Advance - Chemistry (2023 - Paper 1 Online - No. 12)
In a one-litre flask, 6 moles of $A$ undergoes the reaction $A(\mathrm{~g}) \rightleftharpoons P(\mathrm{~g})$. The progress of product formation at two temperatures (in Kelvin), $\mathrm{T}_1$ and $\mathrm{T}_2$, is shown in the figure:
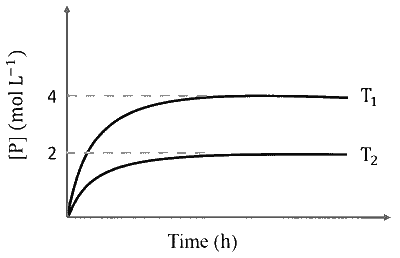
If $\mathrm{T}_1=2 \mathrm{~T}_2$ and $\left(\Delta \mathrm{G}_2^{\Theta}-\Delta \mathrm{G}_1^{\Theta}\right)=\mathrm{RT}_2 \ln \mathrm{x}$, then the value of $\mathrm{x}$ is _______.
$\left[\Delta \mathrm{G}_1^{\Theta}\right.$ and $\Delta \mathrm{G}_2^{\Theta}$ are standard Gibb's free energy change for the reaction at temperatures $\mathrm{T}_1$ and $\mathrm{T}_2$, respectively.]

If $\mathrm{T}_1=2 \mathrm{~T}_2$ and $\left(\Delta \mathrm{G}_2^{\Theta}-\Delta \mathrm{G}_1^{\Theta}\right)=\mathrm{RT}_2 \ln \mathrm{x}$, then the value of $\mathrm{x}$ is _______.
$\left[\Delta \mathrm{G}_1^{\Theta}\right.$ and $\Delta \mathrm{G}_2^{\Theta}$ are standard Gibb's free energy change for the reaction at temperatures $\mathrm{T}_1$ and $\mathrm{T}_2$, respectively.]
Answer
8
Explanation
$\begin{array}{ll}\text { At } \mathrm{T}_1 \mathrm{~K}: & \mathrm{A}(\mathrm{g}) \rightleftharpoons \mathrm{P}(\mathrm{g}) \\\\ \mathrm{t}=0 & 6 \\\\ \mathrm{t}=\infty & 6-\mathrm{x} \quad \mathrm{x}=4 \text { (from plot) }\end{array}$
$\Rightarrow$ At $\mathrm{T}_1 \mathrm{~K}: \mathrm{K}_{\mathrm{P}_1}=\frac{4}{2}=2$
$$ \begin{array}{ll} \text { At } \mathrm{T}_2 \mathrm{~K}: & \mathrm{A}(\mathrm{g}) \rightleftharpoons \mathrm{P}(\mathrm{g}) \\\\ \mathrm{t}=0 & 6 \\\\ \mathrm{t}=\infty & 6-\mathrm{y} \quad \mathrm{y}=2 \text { (from plot) } \end{array} $$
$$ \Rightarrow \text { At } \mathrm{T}_2 \mathrm{~K}: \mathrm{K}_{\mathrm{P}_2}=\frac{2}{4}=\frac{1}{2} $$
Since
$$ \begin{aligned} \Delta \mathrm{G}_1^0 & =-\mathrm{RT}_1 \ln \mathrm{KT}_1 ............(i) \\\\ \Delta \mathrm{G}_2^0 & =-\mathrm{RT}_2 \ln \mathrm{KT}_2 ............(ii) \end{aligned} $$
$\begin{aligned} \Delta \mathrm{G}_2^0-\Delta \mathrm{G}_1^0 & =-\mathrm{RT}_2 \ln \mathrm{KT}_2+\mathrm{RT}_1 \ln \mathrm{KT}_1 \\\\ & =-\mathrm{RT}_2 \ln \frac{1}{2}+\mathrm{RT}_1 \ln 2 \\\\ & =-\mathrm{RT}_2 \ln \frac{1}{2}+\mathrm{R}\left(2 \mathrm{~T}_2\right) \ln 2 \\\\ & =\mathrm{RT}_2 \ln 2+2 \mathrm{RT}_2 \ln 2 \\\\ & =\mathrm{RT}_2 \ln 2+2 \mathrm{RT}_2 \ln 2\end{aligned}$
$\begin{aligned} \Delta \mathrm{G}_2^0-\Delta \mathrm{G}_1^0 & =3 \mathrm{RT}_2 \ln 2 \\\\ & =\mathrm{RT}_2\left(\ln 2^3\right) \\\\ & =\mathrm{RT}_2 \ln 8\end{aligned}$
$\Rightarrow$ At $\mathrm{T}_1 \mathrm{~K}: \mathrm{K}_{\mathrm{P}_1}=\frac{4}{2}=2$
$$ \begin{array}{ll} \text { At } \mathrm{T}_2 \mathrm{~K}: & \mathrm{A}(\mathrm{g}) \rightleftharpoons \mathrm{P}(\mathrm{g}) \\\\ \mathrm{t}=0 & 6 \\\\ \mathrm{t}=\infty & 6-\mathrm{y} \quad \mathrm{y}=2 \text { (from plot) } \end{array} $$
$$ \Rightarrow \text { At } \mathrm{T}_2 \mathrm{~K}: \mathrm{K}_{\mathrm{P}_2}=\frac{2}{4}=\frac{1}{2} $$
Since
$$ \begin{aligned} \Delta \mathrm{G}_1^0 & =-\mathrm{RT}_1 \ln \mathrm{KT}_1 ............(i) \\\\ \Delta \mathrm{G}_2^0 & =-\mathrm{RT}_2 \ln \mathrm{KT}_2 ............(ii) \end{aligned} $$
$\begin{aligned} \Delta \mathrm{G}_2^0-\Delta \mathrm{G}_1^0 & =-\mathrm{RT}_2 \ln \mathrm{KT}_2+\mathrm{RT}_1 \ln \mathrm{KT}_1 \\\\ & =-\mathrm{RT}_2 \ln \frac{1}{2}+\mathrm{RT}_1 \ln 2 \\\\ & =-\mathrm{RT}_2 \ln \frac{1}{2}+\mathrm{R}\left(2 \mathrm{~T}_2\right) \ln 2 \\\\ & =\mathrm{RT}_2 \ln 2+2 \mathrm{RT}_2 \ln 2 \\\\ & =\mathrm{RT}_2 \ln 2+2 \mathrm{RT}_2 \ln 2\end{aligned}$
$\begin{aligned} \Delta \mathrm{G}_2^0-\Delta \mathrm{G}_1^0 & =3 \mathrm{RT}_2 \ln 2 \\\\ & =\mathrm{RT}_2\left(\ln 2^3\right) \\\\ & =\mathrm{RT}_2 \ln 8\end{aligned}$
Comments (0)


