JEE Advance - Chemistry (2023 - Paper 1 Online - No. 11)
One mole of an ideal monoatomic gas undergoes two reversible processes $(\mathrm{A} \rightarrow \mathrm{B}$ and $\mathrm{B} \rightarrow \mathrm{C})$ as shown in the given figure:
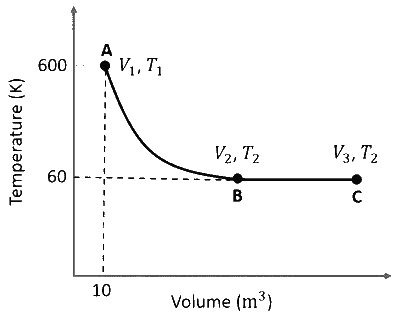
$\mathrm{A} \rightarrow \mathrm{B}$ is an adiabatic process. If the total heat absorbed in the entire process $(\mathrm{A} \rightarrow \mathrm{B}$ and $\mathrm{B} \rightarrow \mathrm{C})$ is $\mathrm{R} T_2 \ln 10$, the value of $2 \log V_3$ is _______.
[Use, molar heat capacity of the gas at constant pressure, $C_{\mathrm{p}, \mathrm{m}}=\frac{5}{2} \mathrm{R}$ ]

$\mathrm{A} \rightarrow \mathrm{B}$ is an adiabatic process. If the total heat absorbed in the entire process $(\mathrm{A} \rightarrow \mathrm{B}$ and $\mathrm{B} \rightarrow \mathrm{C})$ is $\mathrm{R} T_2 \ln 10$, the value of $2 \log V_3$ is _______.
[Use, molar heat capacity of the gas at constant pressure, $C_{\mathrm{p}, \mathrm{m}}=\frac{5}{2} \mathrm{R}$ ]
Answer
7
Explanation
Since $A B$ is Adiabatic process
$$ \begin{aligned} &\Rightarrow \left(\frac{\mathrm{T}_1}{\mathrm{~T}_2}\right) =\left(\frac{\mathrm{V}_2}{\mathrm{~V}_1}\right)^{\mathrm{V}-1} \\\\ &\Rightarrow\mathrm{~T}_1 \mathrm{~V}_1^{\gamma-1} =\mathrm{T}_2 \mathrm{~V}_2^{\gamma-1} \\\\ &\Rightarrow600(10)^{2 / 3} =60\left(\mathrm{~V}_2\right)^{2 / 3} \\\\ &\Rightarrow\left(\mathrm{~V}_2\right)^{2 / 3} =(10)^{5 / 3} \\\\ &\Rightarrow\mathrm{~V}_2 =(10)^{5 / 2} \\\\ &\Rightarrow\mathrm{Q}_{\mathrm{AB}} =0 \end{aligned} $$
$\begin{aligned} \mathrm{Q}_{\mathrm{AC}} & =\mathrm{nRT}_2 \ln \left(\frac{\mathrm{V}_3}{\mathrm{~V}_2}\right) \\\\ & =\mathrm{RT}_2 \ln \left(\frac{\mathrm{V}_3}{\mathrm{~V}_2}\right) .........(i)\end{aligned}$
$\begin{gathered}\text { Total heat absorbed }=\mathrm{RT}_2 \ln \left(\frac{\mathrm{V}_3}{\mathrm{~V}_2}\right) \\\\ =\mathrm{RT}_2 \ln (10) ........(ii)\end{gathered}$
Equating equation (i) and equation (ii)
$$ \begin{aligned} &\mathrm{RT}_2 \ln \left(\frac{\mathrm{V}_3}{\mathrm{~V}_2}\right) =\mathrm{RT}_2 \ln (10) \\\\ &\Rightarrow\ln \left(\frac{\mathrm{V}_3}{\mathrm{~V}_2}\right) =\ln (10) \end{aligned} $$
$$ \mathrm{V}_3=10 \mathrm{~V}_2 $$
Substitute value of $\mathrm{V}_2$
$$ \begin{aligned} & =10(10)^{5 / 2}=(10)^{7 / 2} \\\\ V_3 & =(10)^{7 / 2} \end{aligned} $$
Taking $\log$ on both side, we get
$$ \begin{aligned} &\Rightarrow \log \left(\mathrm{V}_3\right) =\log (10)^{7 / 2} \\\\ &\Rightarrow \log \left(\mathrm{V}_3\right) =\frac{7}{2} \log (10) \\\\ &\Rightarrow 2 \log \left(\mathrm{V}_3\right) =7 \log (10) \\\\ \therefore 2 \log \left(\mathrm{V}_3\right) =7 \end{aligned} $$
$$ \begin{aligned} &\Rightarrow \left(\frac{\mathrm{T}_1}{\mathrm{~T}_2}\right) =\left(\frac{\mathrm{V}_2}{\mathrm{~V}_1}\right)^{\mathrm{V}-1} \\\\ &\Rightarrow\mathrm{~T}_1 \mathrm{~V}_1^{\gamma-1} =\mathrm{T}_2 \mathrm{~V}_2^{\gamma-1} \\\\ &\Rightarrow600(10)^{2 / 3} =60\left(\mathrm{~V}_2\right)^{2 / 3} \\\\ &\Rightarrow\left(\mathrm{~V}_2\right)^{2 / 3} =(10)^{5 / 3} \\\\ &\Rightarrow\mathrm{~V}_2 =(10)^{5 / 2} \\\\ &\Rightarrow\mathrm{Q}_{\mathrm{AB}} =0 \end{aligned} $$
$\begin{aligned} \mathrm{Q}_{\mathrm{AC}} & =\mathrm{nRT}_2 \ln \left(\frac{\mathrm{V}_3}{\mathrm{~V}_2}\right) \\\\ & =\mathrm{RT}_2 \ln \left(\frac{\mathrm{V}_3}{\mathrm{~V}_2}\right) .........(i)\end{aligned}$
$\begin{gathered}\text { Total heat absorbed }=\mathrm{RT}_2 \ln \left(\frac{\mathrm{V}_3}{\mathrm{~V}_2}\right) \\\\ =\mathrm{RT}_2 \ln (10) ........(ii)\end{gathered}$
Equating equation (i) and equation (ii)
$$ \begin{aligned} &\mathrm{RT}_2 \ln \left(\frac{\mathrm{V}_3}{\mathrm{~V}_2}\right) =\mathrm{RT}_2 \ln (10) \\\\ &\Rightarrow\ln \left(\frac{\mathrm{V}_3}{\mathrm{~V}_2}\right) =\ln (10) \end{aligned} $$
$$ \mathrm{V}_3=10 \mathrm{~V}_2 $$
Substitute value of $\mathrm{V}_2$
$$ \begin{aligned} & =10(10)^{5 / 2}=(10)^{7 / 2} \\\\ V_3 & =(10)^{7 / 2} \end{aligned} $$
Taking $\log$ on both side, we get
$$ \begin{aligned} &\Rightarrow \log \left(\mathrm{V}_3\right) =\log (10)^{7 / 2} \\\\ &\Rightarrow \log \left(\mathrm{V}_3\right) =\frac{7}{2} \log (10) \\\\ &\Rightarrow 2 \log \left(\mathrm{V}_3\right) =7 \log (10) \\\\ \therefore 2 \log \left(\mathrm{V}_3\right) =7 \end{aligned} $$
Comments (0)


