JEE Advance - Chemistry (2023 - Paper 1 Online - No. 10)
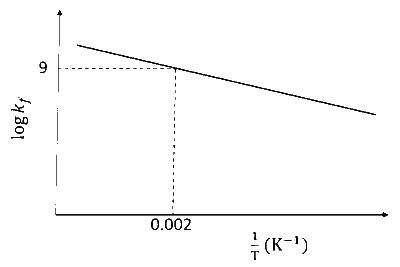
The plot of $\log k_f$ versus $1 / T$ for a reversible reaction $\mathrm{A}(\mathrm{g}) \rightleftharpoons \mathrm{P}(\mathrm{g})$ is shown.
Pre-exponential factors for the forward and backward reactions are $10^{15} \mathrm{~s}^{-1}$ and $10^{11} \mathrm{~s}^{-1}$, respectively. If the value of $\log K$ for the reaction at $500 \mathrm{~K}$ is 6 , the value of $\left|\log k_b\right|$ at $250 \mathrm{~K}$ is ______.
$$ \begin{aligned} & {[K=\text { equilibrium constant of the reaction }} \\\\ & k_f=\text { rate constant of forward reaction } \\\\ & \left.k_b=\text { rate constant of backward reaction }\right] \end{aligned} $$

Pre-exponential factors for the forward and backward reactions are $10^{15} \mathrm{~s}^{-1}$ and $10^{11} \mathrm{~s}^{-1}$, respectively. If the value of $\log K$ for the reaction at $500 \mathrm{~K}$ is 6 , the value of $\left|\log k_b\right|$ at $250 \mathrm{~K}$ is ______.
$$ \begin{aligned} & {[K=\text { equilibrium constant of the reaction }} \\\\ & k_f=\text { rate constant of forward reaction } \\\\ & \left.k_b=\text { rate constant of backward reaction }\right] \end{aligned} $$
Answer
5
Explanation
For reaction $\mathrm{A}(\mathrm{g}) \rightleftharpoons \mathrm{P}(\mathrm{g})$
$\log \mathrm{k}_{\mathrm{f}}=\frac{-\mathrm{E}_{\mathrm{f}}}{2.303 \mathrm{RT}}+\log \mathrm{A}_{\mathrm{f}}$ [Arrhenius equation for forward reaction]
From plot when, $\frac{1}{\mathrm{~T}}=0.002, \log \mathrm{k}_{\mathrm{f}}=9$
$\begin{aligned} & \Rightarrow 9=\frac{-E_f}{2.303 R}(0.002)+\log \left(A_f\right) \\\\ & \text { Given }: A_f=10^{15} \mathrm{~s}^{-1} \\\\ & \Rightarrow 9=\frac{-E_f}{2.303 R}(0.002)+15 \\\\ & \Rightarrow \frac{E_f}{2.303 R}=\frac{6}{0.002}=3000\end{aligned}$
$\begin{aligned} \text { Now, } \mathrm{K} & =\frac{\mathrm{k}_{\mathrm{f}}}{\mathrm{k}_{\mathrm{b}}}=\frac{\mathrm{A}_{\mathrm{f}}}{\mathrm{A}_{\mathrm{b}}} \mathrm{e}^{-\left(\mathrm{E}_{\mathrm{f}}-\mathrm{E}_{\mathrm{b}}\right) / \mathrm{RT}} \\\\ \log \mathrm{K} & =-\frac{1}{2.303} \frac{\left(\mathrm{E}_{\mathrm{f}}-\mathrm{E}_{\mathrm{b}}\right)}{R T}+\log \left(\frac{10^{15}}{10^{11}}\right)\end{aligned}$
At $500 \mathrm{~K}$
$$ \begin{aligned} & \Rightarrow 6=\frac{-\left(\mathrm{E}_{\mathrm{f}}-\mathrm{E}_{\mathrm{b}}\right)}{500 \mathrm{R}(2.303)}+4 \\\\ & \Rightarrow(1000 \mathrm{R})(2.303)=\mathrm{E}_{\mathrm{b}}-\mathrm{E}_{\mathrm{f}} \\\\ & \Rightarrow(1000 \mathrm{R})(2.303)=\mathrm{E}_{\mathrm{b}}-3000(2.303 \mathrm{R}) \\\\ & \Rightarrow \mathrm{E}_{\mathrm{b}}=4000 \mathrm{R}(2.303) ..........(i) \end{aligned} $$
Now $\mathrm{k}_{\mathrm{b}}=\mathrm{A}_{\mathrm{b}} \mathrm{e}^{-\mathrm{E}_{\mathrm{b}} / \mathrm{RT}}$
$\begin{aligned} & \Rightarrow \log \mathrm{k}_{\mathrm{b}}=\frac{-\mathrm{E}_{\mathrm{b}}}{2.303 \mathrm{RT}}+\log \mathrm{A}_{\mathrm{b}} \\\\ & \text { At } 250 \mathrm{~K}, \\\\ & \Rightarrow \log \mathrm{k}_{\mathrm{b}}=-\frac{4000}{250}+\log \left(10^{11}\right) \text { [From equation (1)] } \\\\ & \quad=-16+11=-5 \\\\ & \left|\log \mathrm{k}_{\mathrm{b}}\right|=5\end{aligned}$
$\log \mathrm{k}_{\mathrm{f}}=\frac{-\mathrm{E}_{\mathrm{f}}}{2.303 \mathrm{RT}}+\log \mathrm{A}_{\mathrm{f}}$ [Arrhenius equation for forward reaction]
From plot when, $\frac{1}{\mathrm{~T}}=0.002, \log \mathrm{k}_{\mathrm{f}}=9$
$\begin{aligned} & \Rightarrow 9=\frac{-E_f}{2.303 R}(0.002)+\log \left(A_f\right) \\\\ & \text { Given }: A_f=10^{15} \mathrm{~s}^{-1} \\\\ & \Rightarrow 9=\frac{-E_f}{2.303 R}(0.002)+15 \\\\ & \Rightarrow \frac{E_f}{2.303 R}=\frac{6}{0.002}=3000\end{aligned}$
$\begin{aligned} \text { Now, } \mathrm{K} & =\frac{\mathrm{k}_{\mathrm{f}}}{\mathrm{k}_{\mathrm{b}}}=\frac{\mathrm{A}_{\mathrm{f}}}{\mathrm{A}_{\mathrm{b}}} \mathrm{e}^{-\left(\mathrm{E}_{\mathrm{f}}-\mathrm{E}_{\mathrm{b}}\right) / \mathrm{RT}} \\\\ \log \mathrm{K} & =-\frac{1}{2.303} \frac{\left(\mathrm{E}_{\mathrm{f}}-\mathrm{E}_{\mathrm{b}}\right)}{R T}+\log \left(\frac{10^{15}}{10^{11}}\right)\end{aligned}$
At $500 \mathrm{~K}$
$$ \begin{aligned} & \Rightarrow 6=\frac{-\left(\mathrm{E}_{\mathrm{f}}-\mathrm{E}_{\mathrm{b}}\right)}{500 \mathrm{R}(2.303)}+4 \\\\ & \Rightarrow(1000 \mathrm{R})(2.303)=\mathrm{E}_{\mathrm{b}}-\mathrm{E}_{\mathrm{f}} \\\\ & \Rightarrow(1000 \mathrm{R})(2.303)=\mathrm{E}_{\mathrm{b}}-3000(2.303 \mathrm{R}) \\\\ & \Rightarrow \mathrm{E}_{\mathrm{b}}=4000 \mathrm{R}(2.303) ..........(i) \end{aligned} $$
Now $\mathrm{k}_{\mathrm{b}}=\mathrm{A}_{\mathrm{b}} \mathrm{e}^{-\mathrm{E}_{\mathrm{b}} / \mathrm{RT}}$
$\begin{aligned} & \Rightarrow \log \mathrm{k}_{\mathrm{b}}=\frac{-\mathrm{E}_{\mathrm{b}}}{2.303 \mathrm{RT}}+\log \mathrm{A}_{\mathrm{b}} \\\\ & \text { At } 250 \mathrm{~K}, \\\\ & \Rightarrow \log \mathrm{k}_{\mathrm{b}}=-\frac{4000}{250}+\log \left(10^{11}\right) \text { [From equation (1)] } \\\\ & \quad=-16+11=-5 \\\\ & \left|\log \mathrm{k}_{\mathrm{b}}\right|=5\end{aligned}$
Comments (0)


