Sign In

JEE Advance - Chemistry (2022 - Paper 2 Online - No. 9)

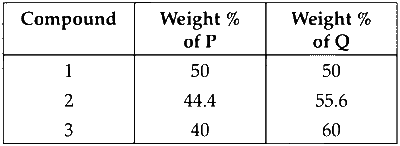
To check the principle of multiple proportions, a series of pure binary compounds $\left(\mathrm{P}_{\mathrm{m}} \mathrm{Q}_{\mathrm{n}}\right)$ were analyzed and their composition is tabulated below. The correct option(s) is(are)

Compound Weight % of $\mathrm{P}$ Weight % of $\mathrm{Q}$
1 50 50
2 44.4 55.6
3 40 60
If empirical formula of compound 3 is $P_{3} Q_{4}$, then the empirical formula of compound 2 is $\mathrm{P}_{3} \mathrm{Q}_{5}$.
If empirical formula of compound 3 is $\mathrm{P}_{3} \mathrm{Q}_{2}$ and atomic weight of element $\mathrm{P}$ is 20 , then the atomic weight of $\mathrm{Q}$ is 45 .
If empirical formula of compound 2 is $P Q$, then the empirical formula of the compound $\mathbf{1}$ is $\mathrm{P}_{5} \mathrm{Q}_{4}$.
If atomic weight of $\mathrm{P}$ and $\mathrm{Q}$ are 70 and 35 , respectively, then the empirical formula of compound $\mathbf{1}$ is $\mathrm{P}_{2} \mathrm{Q}$.

Explanation

JEE Advanced 2022 Paper 2 Online Chemistry - Some Basic Concepts of Chemistry Question 4 English Explanation

(A) If emperical formula of compound 3 is $P_3 Q_4$ then its molar ratio will be $\frac{40}{3} : \frac{60}{4}$

$$ =\frac{40}{3} \times \frac{4}{60}=\frac{16}{18}=0.88 $$

If empirical formula of compound 2 is $\mathrm{P}_3 \mathrm{Q}_5$, then its molar ratio

$$ \begin{aligned} & =\frac{44.4}{2} : {\frac{55.6}{5}} \\\\ & =\frac{44.4}{2} \times \frac{5}{55.6}=2 \end{aligned} $$

Since molar ratio of both the compound is not equal

So, option (A) is not correct.

(B) If empirical formula of compound 3 is $\mathrm{P}_3 \mathrm{Q}_2$, i.e.,

$$ \begin{aligned} & \frac{40}{M_P}: \frac{60}{M_Q}=\frac{3}{2} \\\\ & \Rightarrow \frac{40}{M_P} \times \frac{M_Q}{60}=\frac{3}{2} \end{aligned} $$

$$ \begin{aligned} \Rightarrow \frac{4 \mathrm{M}_{\mathrm{Q}}}{6 \mathrm{M}_{\mathrm{P}}} & =\frac{3}{2} \\\\ \Rightarrow \frac{\mathrm{M}_{\mathrm{Q}}}{\mathrm{M}_{\mathrm{P}}} & =\frac{3}{2} \times \frac{6}{4}=\frac{9}{4} \end{aligned} $$

and $\mathrm{M}_{\mathrm{P}}=20$ (given)

So, $ \frac{\mathrm{M}_{\mathrm{Q}}}{20}=\frac{9}{4}$

$$ \begin{aligned} & \mathrm{M}_{\mathrm{Q}}=\frac{9 \times 26^5}{4} \\\\ & \mathrm{M}_{\mathrm{Q}}=45 \end{aligned} $$

So, option (B) is correct.

(C) If empirical formula of compound 2 is PQ, So the molar ratio is

$$ \frac{44.4}{1}: \frac{55.6}{1}=\frac{44.4}{55.6}=0.79 \sim 0.8 $$

Empirical formula of compound 1 is $P_5 Q_4$

so the molar ratio is $\frac{50}{5} : { } \frac{50}{4}$.

$$ =\frac{50}{5} \times \frac{4}{50}=\frac{4}{5}=0.8 $$

Since, molar ratio of both the compound is equal hence, state $(\mathrm{C})$ is correct.

So, option (C) is correct.

(D) $\mathrm{M}_{\mathrm{P}}=70, \mathrm{M}_{\mathrm{Q}}=35$

Molar ratio of compound 1 is

$$ \begin{aligned} \frac{50}{M_{\mathrm{P}}}: \frac{50}{\mathrm{M}_{\mathrm{Q}}} & =\frac{50}{70}: \frac{50}{35} \\\\ & =\frac{50}{70} \times \frac{35}{50}=\frac{1}{2} \end{aligned} $$

Hence, empirical formula of compound $\mathrm{PQ}_2$.

So, option (D) is incorrect.

Comments (0)

Advertisement