JEE Advance - Chemistry (2022 - Paper 2 Online - No. 3)
Consider the strong electrolytes $Z_{m} X_{n}, U_{m} Y_{p}$ and $V_{m} X_{n}$. Limiting molar conductivity ( $\Lambda^{0}$ ) of $\mathrm{U}_{\mathrm{m}} \mathrm{Y}_{\mathrm{p}}$ and $\mathrm{V}_{\mathrm{m}} \mathrm{X}_{\mathrm{n}}$ are 250 and $440 \mathrm{~S} \mathrm{~cm}^{2} \mathrm{~mol}^{-1}$, respectively. The value of $(\mathrm{m}+\mathrm{n}+\mathrm{p})$ is
Given:
$\lambda^{0}$ is the limiting molar conductivity of ions
The plot of molar conductivity ( $\Lambda$ ) of $\mathrm{Z}_{\mathrm{m}} \mathrm{X}_{\mathrm{n}} v s\, \mathrm{c}^{1 / 2}$ is given below.
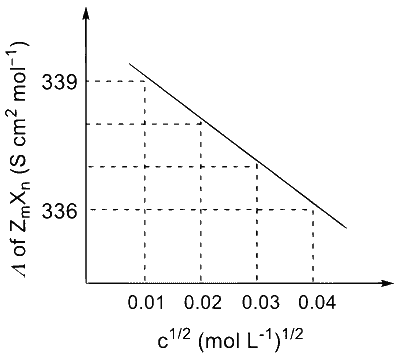
Given:
| Ion | $\mathrm{Z}^{\mathrm{n}+}$ | $\mathrm{U}^{\mathrm{p}+}$ | $\mathrm{V}^{\mathrm{n}+}$ | $\mathrm{X}^{\mathrm{m}-}$ | $\mathrm{Y}^{\mathrm{m}-}$ |
|---|---|---|---|---|---|
| $\lambda^{0}\left(\mathrm{~S} \mathrm{~cm}^{2} \mathrm{~mol}^{-1}\right)$ | $50.0$ | $25.0$ | $100.0$ | $80.0$ | $100.0$ |
$\lambda^{0}$ is the limiting molar conductivity of ions
The plot of molar conductivity ( $\Lambda$ ) of $\mathrm{Z}_{\mathrm{m}} \mathrm{X}_{\mathrm{n}} v s\, \mathrm{c}^{1 / 2}$ is given below.

Answer
7
Explanation
Given,
$\Lambda_{\mathrm{V}_{\mathrm{m}} \mathrm{Y}_{\mathrm{p}}}^{\circ}=250 \mathrm{~S} \mathrm{~cm}^2 \mathrm{~mol}^{-1}$
$\Lambda_{\mathrm{V}_m \mathrm{x}_n}=440 \mathrm{~S} \mathrm{~cm}^2 \mathrm{~mol}^{-1}$
It is also given that
$$ \begin{aligned} & \lambda^{\circ} \mathrm{Z}^{n+}=50 \mathrm{~S} \mathrm{~cm}^2 \mathrm{~mol}^{-1} \\\\ & \lambda_{\mathrm{V} p+}^0=25.0 \mathrm{~S} \mathrm{~cm}^2 \mathrm{~mol}^{-1} \\\\ & \lambda_{\mathrm{V}^{n+}}^{\circ}=100.0 \mathrm{~S} \mathrm{~cm}^2 \mathrm{~mol}^{-1} \\\\ & \lambda_{\mathrm{X}^{m-}}^{\circ}=80.0 \mathrm{~S} \mathrm{~cm}^2 \mathrm{~mol}^{-1} \\\\ & \lambda_{\mathrm{Y}^{m-}}^{\circ}=100.0 \mathrm{~S} \mathrm{~cm}^2 \mathrm{~mol}^{-1} \\\\ \end{aligned} $$
Now, $ \Lambda_{\mathrm{V}_m \mathrm{Y}_p}=m \lambda_{\mathrm{V}^{+}}^{\circ}+p \lambda^{\circ}{ }_{\mathrm{Y}}$
$$ 250=25 m+100 p $$
$$ 10=m+4p $$ ..........(1)
Also, $ \Lambda_{\mathrm{V}_m \mathrm{x}_n}=m \lambda_{\mathrm{v}^{+}}^{\circ}+n \lambda^{\circ} \mathrm{X}^{-}$
$440=100 m+80 n$
$22=5 m+4 n$ ........(2)
In the question, a graph of $(\Lambda)$ of $Z_m X_n$ Vs $C^{1 / 2}$ is given,
We know, $$ \lambda_m=\lambda_m^0-A \sqrt{C} $$
For electrolyte $Z_m X_n$ and from given curve
$$ \begin{aligned} & \lambda_m\left(Z_m X_n\right)=\lambda_m^0\left(Z_m X_n\right)-A \sqrt{C} \\\\ & -A=\frac{336-339}{0.04-0.01}=-\frac{3}{0.03} \\\\ & \Rightarrow A=100 \\\\ & \therefore \text { For } \lambda_m=336 \mathrm{~S} \mathrm{~cm}^2 \mathrm{~mol}^{-1} \\\\ & \Rightarrow 336=\lambda_m^{\circ}\left(Z_m X_n\right)-100 \times 0.04 \\\\ & \lambda_m^{\circ}=336+4=340 \mathrm{~S} \mathrm{~cm}{ }^2 \mathrm{~mol}^{-1} \end{aligned} $$
So,
$$ \begin{aligned} \Lambda_{Z_m x_n} & =m \lambda_{\mathrm{Z}^{+}}+n \lambda_{\mathrm{X}^{-}} \\\\ 340 & =50 m+80 n \\\\ 34 & =5 m+8 n ........(3) \end{aligned} $$
Solving eqn (2) and eqn (3),
$n=\frac{12}{4}=3 $
$$ \Rightarrow $$ $n=3$
Substituting the value of $n$ in eqn (2), we get,
$$ \begin{aligned} 22 & =5 m+4(3) \\\\ \Rightarrow 22 & =5 m+12 \\\\ \Rightarrow 5 m & =22-12=10 \\\\ \Rightarrow m & =\frac{10}{5}=2 \\\\ \Rightarrow m & =2 \end{aligned} $$
Now, substituting the value of $m$ is eqn $(1)$, we get
$$ \begin{aligned} 10 & =m+4 p \\\\ \Rightarrow 10 & =2+4 p \\\\ \Rightarrow 8 & =4 p \\\\ \Rightarrow p & =\frac{8}{4}=2 \\\\ \Rightarrow p & =22 \end{aligned} $$
So, $m+n+p=2+3+2$
$$\Rightarrow m+n+p=7 $$
Hence, the required value of $m+n+p$ is 7 .
$\Lambda_{\mathrm{V}_{\mathrm{m}} \mathrm{Y}_{\mathrm{p}}}^{\circ}=250 \mathrm{~S} \mathrm{~cm}^2 \mathrm{~mol}^{-1}$
$\Lambda_{\mathrm{V}_m \mathrm{x}_n}=440 \mathrm{~S} \mathrm{~cm}^2 \mathrm{~mol}^{-1}$
It is also given that
$$ \begin{aligned} & \lambda^{\circ} \mathrm{Z}^{n+}=50 \mathrm{~S} \mathrm{~cm}^2 \mathrm{~mol}^{-1} \\\\ & \lambda_{\mathrm{V} p+}^0=25.0 \mathrm{~S} \mathrm{~cm}^2 \mathrm{~mol}^{-1} \\\\ & \lambda_{\mathrm{V}^{n+}}^{\circ}=100.0 \mathrm{~S} \mathrm{~cm}^2 \mathrm{~mol}^{-1} \\\\ & \lambda_{\mathrm{X}^{m-}}^{\circ}=80.0 \mathrm{~S} \mathrm{~cm}^2 \mathrm{~mol}^{-1} \\\\ & \lambda_{\mathrm{Y}^{m-}}^{\circ}=100.0 \mathrm{~S} \mathrm{~cm}^2 \mathrm{~mol}^{-1} \\\\ \end{aligned} $$
Now, $ \Lambda_{\mathrm{V}_m \mathrm{Y}_p}=m \lambda_{\mathrm{V}^{+}}^{\circ}+p \lambda^{\circ}{ }_{\mathrm{Y}}$
$$ 250=25 m+100 p $$
$$ 10=m+4p $$ ..........(1)
Also, $ \Lambda_{\mathrm{V}_m \mathrm{x}_n}=m \lambda_{\mathrm{v}^{+}}^{\circ}+n \lambda^{\circ} \mathrm{X}^{-}$
$440=100 m+80 n$
$22=5 m+4 n$ ........(2)
In the question, a graph of $(\Lambda)$ of $Z_m X_n$ Vs $C^{1 / 2}$ is given,
We know, $$ \lambda_m=\lambda_m^0-A \sqrt{C} $$
For electrolyte $Z_m X_n$ and from given curve
$$ \begin{aligned} & \lambda_m\left(Z_m X_n\right)=\lambda_m^0\left(Z_m X_n\right)-A \sqrt{C} \\\\ & -A=\frac{336-339}{0.04-0.01}=-\frac{3}{0.03} \\\\ & \Rightarrow A=100 \\\\ & \therefore \text { For } \lambda_m=336 \mathrm{~S} \mathrm{~cm}^2 \mathrm{~mol}^{-1} \\\\ & \Rightarrow 336=\lambda_m^{\circ}\left(Z_m X_n\right)-100 \times 0.04 \\\\ & \lambda_m^{\circ}=336+4=340 \mathrm{~S} \mathrm{~cm}{ }^2 \mathrm{~mol}^{-1} \end{aligned} $$
So,
$$ \begin{aligned} \Lambda_{Z_m x_n} & =m \lambda_{\mathrm{Z}^{+}}+n \lambda_{\mathrm{X}^{-}} \\\\ 340 & =50 m+80 n \\\\ 34 & =5 m+8 n ........(3) \end{aligned} $$
Solving eqn (2) and eqn (3),
$n=\frac{12}{4}=3 $
$$ \Rightarrow $$ $n=3$
Substituting the value of $n$ in eqn (2), we get,
$$ \begin{aligned} 22 & =5 m+4(3) \\\\ \Rightarrow 22 & =5 m+12 \\\\ \Rightarrow 5 m & =22-12=10 \\\\ \Rightarrow m & =\frac{10}{5}=2 \\\\ \Rightarrow m & =2 \end{aligned} $$
Now, substituting the value of $m$ is eqn $(1)$, we get
$$ \begin{aligned} 10 & =m+4 p \\\\ \Rightarrow 10 & =2+4 p \\\\ \Rightarrow 8 & =4 p \\\\ \Rightarrow p & =\frac{8}{4}=2 \\\\ \Rightarrow p & =22 \end{aligned} $$
So, $m+n+p=2+3+2$
$$\Rightarrow m+n+p=7 $$
Hence, the required value of $m+n+p$ is 7 .
Comments (0)


