JEE Advance - Chemistry (2022 - Paper 2 Online - No. 2)
An aqueous solution is prepared by dissolving $0.1 \mathrm{~mol}$ of an ionic salt in $1.8 \mathrm{~kg}$ of water at $35^{\circ} \mathrm{C}$. The salt remains $90 \%$ dissociated in the solution. The vapour pressure of the solution is $59.724 \mathrm{~mm}$ of Hg. Vapor pressure of water at $35{ }^{\circ} \mathrm{C}$ is $60.000 \mathrm{~mm}$ of $\mathrm{Hg}$. The number of ions present per formula unit of the ionic salt is _________.
Answer
5
Explanation
Vapour pressure of solution $\left(\mathrm{P}_{\mathrm{A}}\right)$
$$
=59.724 \mathrm{~mm} \text { of } \mathrm{Hg}
$$
Vapour pressure of pure water $\left(\mathrm{P}_{\mathrm{A}}^{\circ}\right)$ $$ =60.000 \mathrm{~mm} \text { of } \mathrm{Hg} $$
Also, $0.1 \mathrm{~mol}$ of an ionic solid is dissolved in $1.8 \mathrm{~kg}$ of water and salt remains $90 \%$ dissocated in the solution.
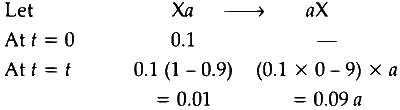
So, total number of moles $=0.01+0.09 a$ of non-volatile particles.
Now, mass of water $=1.8 \mathrm{~kg}=1.8 \times 1.8 \times 1000 \mathrm{~g}$
Molar mass of water $=18 \mathrm{~g}$
Moles of water $=\frac{1.8 \times 1000}{18}=100$ moles
Using the colligative property, relative lowering in vapour pressure,
$$ \frac{\mathrm{P}_{\mathrm{A}}^{\circ}-\mathrm{P}_{\mathrm{A}}}{\mathrm{P}_{\mathrm{A}}^{\circ}}=x_{\mathrm{A}} $$
$$ \Rightarrow $$ $\frac{60-59.724}{60} =\frac{0.01+0.09 a}{100} $
$$ \Rightarrow $$ $ \frac{0.276}{60} =\frac{0.01+0.09 a}{100} $
$$ \Rightarrow $$ $ \frac{27.6}{60} =0.01+0.09 a $
$$ \Rightarrow $$ $ 0.46 =0.01+0.09 a $
$$ \Rightarrow $$ $ 0.09 a =0.45 $
$$ \Rightarrow $$ $ a =\frac{0.45}{0.89} $
$$ \Rightarrow $$ $ a =5 $
So, the number of ions present per formula unit of the ionic salt is 5 .
Vapour pressure of pure water $\left(\mathrm{P}_{\mathrm{A}}^{\circ}\right)$ $$ =60.000 \mathrm{~mm} \text { of } \mathrm{Hg} $$
Also, $0.1 \mathrm{~mol}$ of an ionic solid is dissolved in $1.8 \mathrm{~kg}$ of water and salt remains $90 \%$ dissocated in the solution.
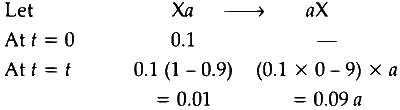
So, total number of moles $=0.01+0.09 a$ of non-volatile particles.
Now, mass of water $=1.8 \mathrm{~kg}=1.8 \times 1.8 \times 1000 \mathrm{~g}$
Molar mass of water $=18 \mathrm{~g}$
Moles of water $=\frac{1.8 \times 1000}{18}=100$ moles
Using the colligative property, relative lowering in vapour pressure,
$$ \frac{\mathrm{P}_{\mathrm{A}}^{\circ}-\mathrm{P}_{\mathrm{A}}}{\mathrm{P}_{\mathrm{A}}^{\circ}}=x_{\mathrm{A}} $$
$$ \Rightarrow $$ $\frac{60-59.724}{60} =\frac{0.01+0.09 a}{100} $
$$ \Rightarrow $$ $ \frac{0.276}{60} =\frac{0.01+0.09 a}{100} $
$$ \Rightarrow $$ $ \frac{27.6}{60} =0.01+0.09 a $
$$ \Rightarrow $$ $ 0.46 =0.01+0.09 a $
$$ \Rightarrow $$ $ 0.09 a =0.45 $
$$ \Rightarrow $$ $ a =\frac{0.45}{0.89} $
$$ \Rightarrow $$ $ a =5 $
So, the number of ions present per formula unit of the ionic salt is 5 .
Comments (0)


