JEE Advance - Chemistry (2022 - Paper 1 Online - No. 15)

Match the rate expressions in LIST-I for the decomposition of $X$ with the corresponding profiles provided in LIST-II. $X_{\mathrm{s}}$ and $\mathrm{k}$ are constants having appropriate units.

List-I	List-II
(I) rate $=\frac{\mathrm{k}[\mathrm{X}]}{\mathrm{X}_{\mathrm{s}}+[\mathrm{X}]}$ under all possible initial concentrations of $\mathrm{X}$	(P)
(II) rate $=\frac{k[X]}{X_{s}+[X]}$ where initial concentrations of $X$ are much less than $X_{s}$	(Q)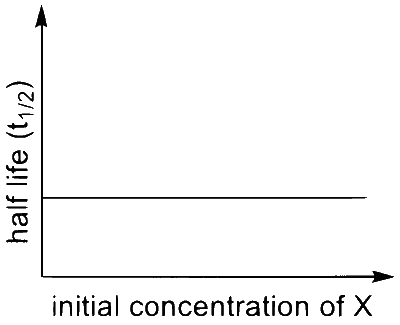
(III) rate $=\frac{k[X]}{X_{s}+[X]}$ where initial concentrations of $\mathrm{X}$ are much higher than $X_{s}$	(R)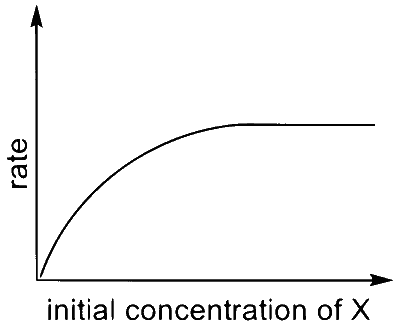
(IV) rate $=\frac{k[X]^{2}}{X_{s}+[X]}$ where initial concentration of $X$ is much higher than $\mathrm{X}_{\mathrm{s}}$	(S)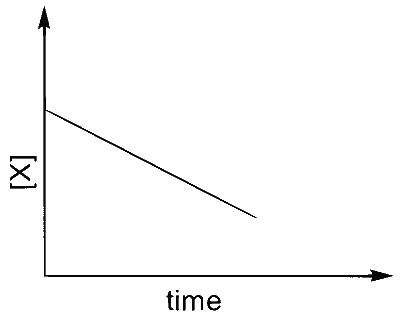
	(T)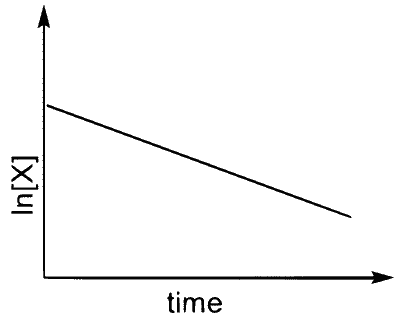

$\mathrm{I} \rightarrow \mathrm{P}$; II $\rightarrow$ Q; III $\rightarrow \mathrm{S}$; IV $\rightarrow \mathrm{T}$

$\mathrm{I} \rightarrow \mathrm{R}$; II $\rightarrow \mathrm{S}$; III $\rightarrow \mathrm{S}$; IV $\rightarrow \mathrm{T}$

$\mathrm{I} \rightarrow \mathrm{P}$; II $\rightarrow$ Q; III $\rightarrow$ Q; IV $\rightarrow$ R

$\mathrm{I} \rightarrow \mathrm{R}$; II $\rightarrow \mathrm{S}$; III $\rightarrow$ Q; IV $\rightarrow \mathrm{R}$

Explanation

rate = $$\frac{k[x]}{X_s+[X]}$$

Case-1 : $$[X] > > {X_s};[X] + {X_s} \approx [X]$$

rate $$ = {{k[X]} \over {[X]}} = k$$ (Zero order w.r.t. X)

I $$\to$$ P, S

Case 2 : $$[X] < < {X_s};[X] + {X_s} \approx {X_s}$$

$$\therefore$$ rate $$ = {{k[X]} \over {{X_s}}} = k'[X]$$ (1^st order w.r.t. X)

$$\therefore$$ I $$\to$$ Q, T

Case-3 : $$[X] \approx {X_s}$$

rate $$ = {{k[X]} \over {{X_s} + [X]}}$$

In this case curve-R given in List-II will match.

$$\therefore$$ I $$\to$$ P, Q, R, S, T (The graph of half-life should start from origin)

(II) rate $$ = {{k[X]} \over {{X_s} + [X]}}$$

$$\because$$ $$[X] < < {X_s}$$

$$\therefore$$ $${X_s} + [X] \approx {X_s}$$

$$\therefore$$ Rate $$ = {{k[X]} \over {{X_s}}} = k'[X]$$ (1^st order w.r.t. X)

$$\therefore$$ II $$\to$$ Q, T

(III) rate $$ = {{k[X]} \over {{X_s} + [X]}}$$

$$\because$$ $$[X] > > {X_s}$$

$$\therefore$$ $${X_s} + [X] \approx [X]$$

$$\therefore$$ rate $$ = {{k[X]} \over {[X]}} = k$$ (Zero order w.r.t. X)

$$\therefore$$ III $$\to$$ P, S

(IV) rate $$ = {{k{{[X]}^2}} \over {{X_s} + [X]}}$$

$$\because$$ $$[X] > > {X_s}$$

$$\therefore$$ $${X_s} + [X] \approx [X]$$

$$\therefore$$ rate $$ = {{k{{[X]}^2}} \over {[X]}} = k[X]$$ (1^st order w.r.t. X)

$$\therefore$$ IV $$\to$$ Q, T

JEE Advance - Chemistry (2022 - Paper 1 Online - No. 15)

Explanation

Comments (0)