For the given reaction,

$$ \mathrm{X}(\mathrm{s}) \rightleftharpoons \mathrm{X}(\mathrm{s})+\mathrm{Z}(\mathrm{g}) $$

We have

$$ \frac{d(\ln K)}{d(1 / T)}=\frac{-\Delta H^{\circ}}{R} $$

And $$ K=\frac{p_{z}}{p^{\circ}} $$

Substituting the value of $$K$$ in Eq. (1), we get

$$ \frac{d\left(\ln \frac{p_{z}}{p^{\circ}}\right)}{d\left(\frac{1}{T}\right)}=\frac{-\Delta H^{\circ}}{R} $$

Or

$$ d\left(\ln \frac{p_{z}}{p^{\circ}}\right)=\frac{-\Delta H^{\circ}}{R} d\left(\frac{1}{T}\right) $$

Integrating both sides of Eq. (2), we get

$$ \ln \frac{p_{z}}{p^{\circ}}=\frac{-\Delta H^{\circ}}{R T}+\ln A $$

Where $$\ln A=$$ Integration constant

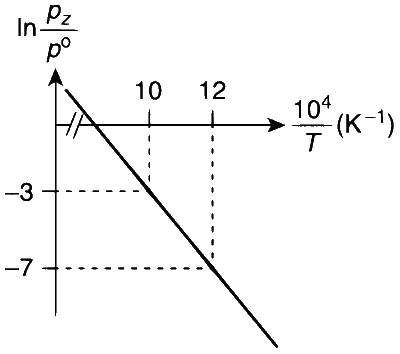
We can also calculate the intercept $$(\ln A)$$ from the plot of $$\ln \frac{p_{z}}{p^{\circ}} \mathrm{vs} \frac{1}{T}$$.

Now, from the equation of straight line, we have

or

$$ \begin{aligned} &y=m x+C \\ &C=y-m x \end{aligned} $$

From the plot, we have

$$ m=-2 \times 10^{4} \mathrm{~K}, y=-3, x=\frac{10}{10^{4}} \mathrm{~K} $$

Now, substituting the above values in Eq. (4), we get

$$ \begin{aligned} &C=-3-\left(-2 \times 10^{4} \times \frac{10}{10^{4}}\right) \\ &C=-3+20 \\ &C=17 \end{aligned} $$

$$\Rightarrow C=17$$

This intercept is equal to $$\ln A$$ in Eq. (3), so we have

$$ \ln A=C=17 $$

From the thermodynamic equations, we have

$$ \Delta G^{\circ}=\Delta H^{\circ}-7 \Delta S^{\circ} $$

For any equilibrium reaction, the Gibb's energy is,

$$ \Delta G^{\circ}=-R T \ln K $$

On comparing both the equations, we get

$$ -R T \ln K=\Delta H^{\circ}-T \Delta S^{\circ} $$

Or

$$ \begin{aligned} \ln K &=\frac{-\Delta H^{\circ}}{R T}+\frac{\Delta S^{\circ}}{R} \\ \left(\frac{p_{z}}{p^{\circ}}\right) &=\frac{-\Delta H^{\circ}}{R T}+\frac{\Delta S^{\circ}}{R} \end{aligned} $$

On comparing Eq. (3) and (6), we have

$$ \frac{\Delta S^{\circ}}{R}=\ln A=17 $$

Or

$$ \begin{aligned} \Delta S^{\circ} &=17 R \\ &=17 \times 8.314 \\ &=141.34 \,\mathrm{JK}^{-1} \end{aligned} $$