Sign In

JEE Advance - Chemistry (2021 - Paper 1 Online - No. 7)

For the reaction, X(s) $$\rightleftharpoons$$ Y(s) + Z(g), the plot of $$\ln {{pz} \over {{p^\theta }}}$$ versus $${{{{10}^4}} \over T}$$ is given below (in solid line), where pz is the pressure (in bar) of the gas Z at temperature T and $${{p^\theta }}$$ = 1 bar.


(Given, $${{d(\ln K)} \over {d\left( {{1 \over T}} \right)}} = - {{\Delta {H^\theta }} \over R}$$, where the equilibrium
constant, $$K = {{pz} \over {{p^\theta }}}$$ and the gas constant, R = 8.314 J K$$-$$1 mol$$-$$1)
For the reaction, X(s) $$\rightleftharpoons$$ Y(s) + Z(g), the plot of $$\ln {{pz} \over {{p^\theta }}}$$ versus $${{{{10}^4}} \over T}$$ is given below (in solid line), where pz is the pressure (in bar) of the gas Z at temperature T and $${{p^\theta }}$$ = 1 bar.


(Given, $${{d(\ln K)} \over {d\left( {{1 \over T}} \right)}} = - {{\Delta {H^\theta }} \over R}$$, where the equilibrium
constant, $$K = {{pz} \over {{p^\theta }}}$$ and the gas constant, R = 8.314 J K$$-$$1 mol$$-$$1)
For the reaction, X(s) $$\rightleftharpoons$$ Y(s) + Z(g), the plot of $$\ln {{pz} \over {{p^\theta }}}$$ versus $${{{{10}^4}} \over T}$$ is given below (in solid line), where pz is the pressure (in bar) of the gas Z at temperature T and $${{p^\theta }}$$ = 1 bar.


(Given, $${{d(\ln K)} \over {d\left( {{1 \over T}} \right)}} = - {{\Delta {H^\theta }} \over R}$$, where the equilibrium
constant, $$K = {{pz} \over {{p^\theta }}}$$ and the gas constant, R = 8.314 J K$$-$$1 mol$$-$$1)
The value of standard enthalpy, $$\Delta$$Ho (in kJ mol$$-$$1) for the given reaction is _______.
Answer
166.28

Explanation

For the given reaction,

$$ \mathrm{X}(\mathrm{s}) \rightleftharpoons \mathrm{X}(\mathrm{s})+\mathrm{Z}(\mathrm{g}) $$

We have

$$ \frac{d(\ln K)}{d(1 / T)}=\frac{-\Delta H^{\circ}}{R} $$

And $$ K=\frac{p_{z}}{p^{\circ}} $$

Substituting the value of $$K$$ in Eq. (1), we get

$$ \frac{d\left(\ln \frac{p_{z}}{p^{\circ}}\right)}{d\left(\frac{1}{T}\right)}=\frac{-\Delta H^{\circ}}{R} $$

Or

$$ d\left(\ln \frac{p_{z}}{p^{\circ}}\right)=\frac{-\Delta H^{\circ}}{R} d\left(\frac{1}{T}\right) $$

Integrating both sides of Eq. (2), we get

$$ \ln \frac{p_{z}}{p^{\circ}}=\frac{-\Delta H^{\circ}}{R T}+\ln A $$

Where $$\ln A=$$ Integration constant

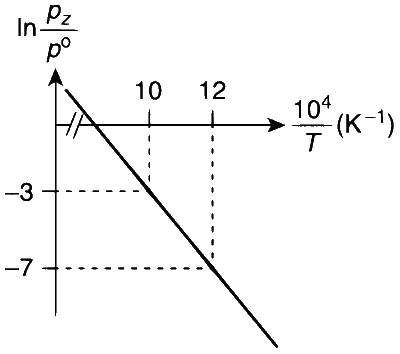
From the given plot of $$\ln \frac{p_{z}}{p^{\circ}} \mathrm{vs} \frac{10^{4}}{T}$$

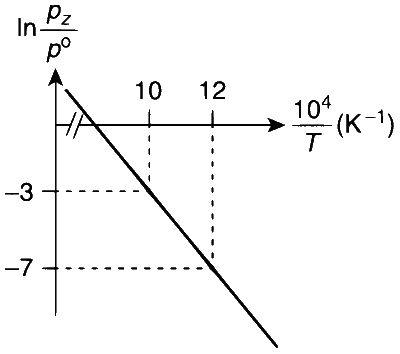
JEE Advanced 2021 Paper 1 Online Chemistry - Thermodynamics Question 18 English Explanation
The slope of the plot is

$$ \text { Slope }=\frac{-\Delta H^{\circ}}{R}=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{-7-(-3)}{\left(\frac{12}{10^{4}}-\frac{10}{10^{4}}\right)} $$

$$\frac{-\Delta H^{\circ}}{R}=\frac{-4}{2} \times 10^{4}$$

$$\Delta H^{\circ}=-2 \times 10^{4} \times R$$

$$\Delta H^{\circ}=2 \times 8.314 \times 10^{4}$$

$$\Delta H^{\circ}=16.628 \times 10^{4} \mathrm{~J} \mathrm{~mol}^{-1}$$

$$\Delta H^{\circ}=166.28 \mathrm{~kJ} \mathrm{~mol}^{-1}$$

Comments (0)

Advertisement