JEE Advance - Chemistry (2021 - Paper 1 Online - No. 5)
For the following reaction scheme, percentage yields are given along the arrow:
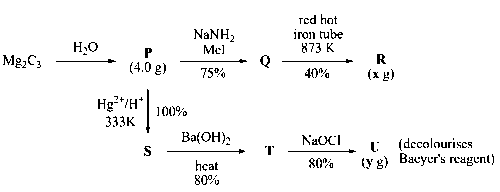
x g and y g are mass of R and U, respectively.
(Use : Molar mass (in g mol$$-$$1) of H, C and O as 1, 12 and 16, respectively)
The value of x is ________.

x g and y g are mass of R and U, respectively.
(Use : Molar mass (in g mol$$-$$1) of H, C and O as 1, 12 and 16, respectively)
The value of x is ________.
Answer
1.62
Explanation
Mg2C3 reacts with water to give propyne.
$$M{g_2}{C_3} + 4{H_2}O \to 2Mg{(OH)_2} + C{H_3} - \mathop {\mathop C\limits_{(P)} }\limits_{{\mathop{\rm Propyne}\nolimits} } \equiv CH$$
Sodium amide (NaNH2) takes proton from alkyne to form acetylide ion which, attacks on Me$$-$$I to give an alkyne with one more carbon.
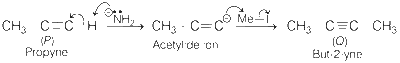
Mass of P formed = 4.0 g
Molar mass of P formed = 40 g mol$$-$$1
Number of moles of P = $${{Mass\,of\,P(W)} \over {Molar\,mass\,of\,P(M)}} = {4 \over {40}} = 0.1$$ mol
1 mole of P forms 75% i.e., 0.75 = 0.075 mole of Q
Polymerisation of alkyne (Butyne) occurs in presence of red hot iron tube to form benzene derivative.
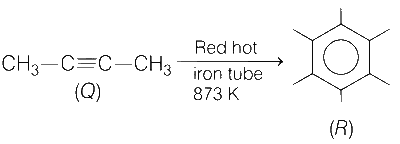
3 moles of alkyne forms 40% i.e., 0.40 mole of benzene derivative, R.
0.075 mole of Q forms $${{0.40} \over 3} \times 0.075 = 0.01$$ mole of R.
Molar mass of R = 162 g/mol
Mass of R formed or value of x = Molar mass $$\times$$ Number of moles = 162 $$\times$$ 0.01 = 1.62 g
$$M{g_2}{C_3} + 4{H_2}O \to 2Mg{(OH)_2} + C{H_3} - \mathop {\mathop C\limits_{(P)} }\limits_{{\mathop{\rm Propyne}\nolimits} } \equiv CH$$
Sodium amide (NaNH2) takes proton from alkyne to form acetylide ion which, attacks on Me$$-$$I to give an alkyne with one more carbon.
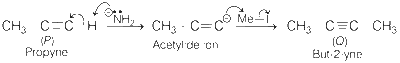
Mass of P formed = 4.0 g
Molar mass of P formed = 40 g mol$$-$$1
Number of moles of P = $${{Mass\,of\,P(W)} \over {Molar\,mass\,of\,P(M)}} = {4 \over {40}} = 0.1$$ mol
1 mole of P forms 75% i.e., 0.75 = 0.075 mole of Q
Polymerisation of alkyne (Butyne) occurs in presence of red hot iron tube to form benzene derivative.

3 moles of alkyne forms 40% i.e., 0.40 mole of benzene derivative, R.
0.075 mole of Q forms $${{0.40} \over 3} \times 0.075 = 0.01$$ mole of R.
Molar mass of R = 162 g/mol
Mass of R formed or value of x = Molar mass $$\times$$ Number of moles = 162 $$\times$$ 0.01 = 1.62 g
Comments (0)


