JEE Advance - Chemistry (2021 - Paper 1 Online - No. 3)
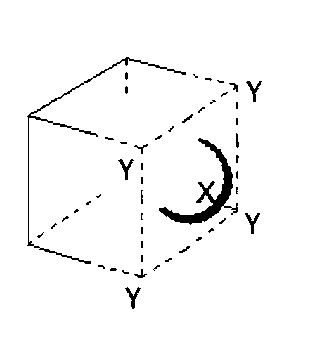
For the given close packed structure of a salt made of cation X and anion Y shown below (ions of only one face are shown for clarity), the packing fraction is approximately (packing fraction = $${{packing\,efficiency} \over {100}}$$)

0.74
0.63
0.52
0.48
Explanation

Radius of cation X = r+
Number of cation X present = $$6 \times {1 \over 2} = 3$$
Radius of anion Y = r$$-$$
Number of anion Y present = $${1 \over 8} \times 8 = 1$$
Side of unit cell = a
As two anions are touching each other, so side of unit cell,
a = 2r$$-$$
Volume of unit cell = a3 = (2r$$-$$)3 = 8r$$_ - ^3$$
Volume of cations X = Number of cation $$\times$$ Volume of one cation = 3 $$\times$$ $${4 \over 3}\pi r_ + ^3$$
Volume of anions Y = Number of anion $$\times$$ Volume of one anion = 1 $$\times$$ $${4 \over 3}\pi r_ - ^3$$
Radius ratio for close packed structure, $${{{r_ + }} \over {{r_ - }}} = 0.414$$
Packing efficiency = $${{Volume\,of\,cation \times Number\,of\,cations + Volume\,of\,anion \times Number\,of\,anions} \over {Volume\,of\,unit\,cell}} \times 100$$
Packing fraction = $${{Packing\,efficiency} \over {100}}$$
$$ = {{1 \times {4 \over 3}\pi r_ - ^3 + 3 \times {4 \over 3}\pi r_ + ^3} \over {8r_ - ^3}}$$
$$ = {{4\pi } \over {3 \times 8}}\left[ {{{r_ - ^3} \over {r_ - ^3}} + {{3r_ + ^3} \over {r_ - ^3}}} \right] = {\pi \over 6}[1 + 3{(0.414)^3}]$$
$$ = {{3.14} \over 6}(1 + 3 \times 0.0710) = {{3.14} \over 6} \times 1.213 = 0.63$$
Comments (0)


