JEE Advance - Chemistry (2020 - Paper 1 Offline - No. 14)
Consider the reaction,
A $$\rightleftharpoons $$ B
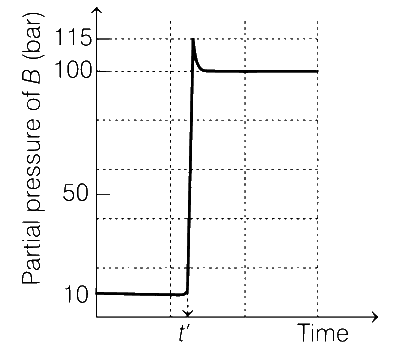
at 1000 K. At time t', the temperature of the system was increased to 2000 K and the system was allowed to reach equilibrium. Throughout this experiment the partial pressure of A was maintained at 1 bar. Given, below is the plot of the partial pressure of B with time. What is the ratio of the standard Gibbs energy of the reaction at 1000 K to that at 2000 K?
A $$\rightleftharpoons $$ B
at 1000 K. At time t', the temperature of the system was increased to 2000 K and the system was allowed to reach equilibrium. Throughout this experiment the partial pressure of A was maintained at 1 bar. Given, below is the plot of the partial pressure of B with time. What is the ratio of the standard Gibbs energy of the reaction at 1000 K to that at 2000 K?

Answer
0.25
Explanation
Given : Image
Using $$\Delta G = \Delta {G^o} + RT\ln {K_p}$$
At equilibrium : $$\Delta {G^o} = - RT\ln {K_p}$$
$$\Delta G_1^0 = - R{T_1}\ln {K_{p1}}$$ ... (i)
$$\Delta G_2^0 = - R{T_2}\ln {K_{p2}}$$ ...(ii)
From Eqs. (i) and (ii),
$${{\Delta G_1^o} \over {\Delta G_2^o}} = {{{T_1}} \over {{T_2}}} \times {{\ln K{p_1}} \over {\ln K{p_2}}}$$
$$ = {{1000} \over {2000}} \times {{\ln (10)} \over {\ln (100)}} = {1 \over 4} = 0.25$$
Using $$\Delta G = \Delta {G^o} + RT\ln {K_p}$$
At equilibrium : $$\Delta {G^o} = - RT\ln {K_p}$$
$$\Delta G_1^0 = - R{T_1}\ln {K_{p1}}$$ ... (i)
$$\Delta G_2^0 = - R{T_2}\ln {K_{p2}}$$ ...(ii)
From Eqs. (i) and (ii),
$${{\Delta G_1^o} \over {\Delta G_2^o}} = {{{T_1}} \over {{T_2}}} \times {{\ln K{p_1}} \over {\ln K{p_2}}}$$
$$ = {{1000} \over {2000}} \times {{\ln (10)} \over {\ln (100)}} = {1 \over 4} = 0.25$$
Comments (0)


