JEE Advance - Chemistry (2019 - Paper 1 Offline - No. 15)
Consider the kinetic data given in the following table for the reaction A + B + C $$ \to $$ Product.
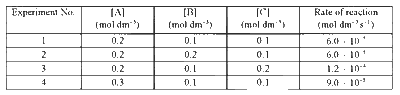
The rate of the reaction for [A] = 0.15 mol dm-3, [B] = 0.25 mol dm-3 and [C] = 0.15 mol dm-3 is found to be Y $$ \times $$ 10-5 mol dm-3s-1. The value of Y is .................

The rate of the reaction for [A] = 0.15 mol dm-3, [B] = 0.25 mol dm-3 and [C] = 0.15 mol dm-3 is found to be Y $$ \times $$ 10-5 mol dm-3s-1. The value of Y is .................
Answer
6.75
Explanation
Rate = $$k{[A]^x}{[B]^y}{[C]^z}$$
$${{{{(Rate)}_1}} \over {{{(Rate)}_2}}} = {{{{[0.2]}^x}{{[0.1]}^y}{{[0.1]}^z}} \over {{{[0.2]}^x}{{[0.2]}^y}{{[0.1]}^z}}} = {{6 \times {{10}^{ - 5}}} \over {6 \times {{10}^{ - 5}}}}$$
$$ \Rightarrow $$ y = 0
$${{{{(Rate)}_1}} \over {{{(Rate)}_3}}} = {{{{[0.2]}^x}{{[0.1]}^y}{{[0.1]}^z}} \over {{{[0.2]}^x}{{[0.1]}^y}{{[0.2]}^z}}} = {{6 \times {{10}^{ - 5}}} \over {1.2 \times {{10}^{ - 4}}}}$$
$$ \Rightarrow $$ z = 1
$${{{{(Rate)}_1}} \over {{{(Rate)}_4}}} = {{{{[0.2]}^x}{{[0.1]}^y}{{[0.1]}^z}} \over {{{[0.3]}^x}{{[0.1]}^y}{{[0.1]}^z}}} = {{6 \times {{10}^{ - 5}}} \over {9 \times {{10}^{ - 5}}}}$$
$$ \Rightarrow $$ x = 1
So, rate = k[A]1[C]1
From exp-Ist,
Rate = $$6.0 \times {10^{ - 5}}$$ mol dm$$ - $$3 s$$ - $$1
6.0 $$ \times $$ 10$$ - $$5 = k[0.2]1[0.1]1
k = 3 $$ \times $$ 10$$ - $$3
Given, [A] = 0.15 mol dm$$ - $$3
[B] = 0.25 mol dm$$ - $$3
[C] = 0.15 mol dm$$ - $$3
$$ \therefore $$ Rate = (3 $$ \times $$ 10$$ - $$3) $$ \times $$ [0.15]1[0.25]0[0.15]1
= 3 $$ \times $$ 10$$ - $$3 $$ \times $$ 0.15 $$ \times $$ 0.15
Rate = 6.75 $$ \times $$ 10$$ - $$5 mol dm$$ - $$3 s$$ - $$1
Thus, Y = 6.75
$${{{{(Rate)}_1}} \over {{{(Rate)}_2}}} = {{{{[0.2]}^x}{{[0.1]}^y}{{[0.1]}^z}} \over {{{[0.2]}^x}{{[0.2]}^y}{{[0.1]}^z}}} = {{6 \times {{10}^{ - 5}}} \over {6 \times {{10}^{ - 5}}}}$$
$$ \Rightarrow $$ y = 0
$${{{{(Rate)}_1}} \over {{{(Rate)}_3}}} = {{{{[0.2]}^x}{{[0.1]}^y}{{[0.1]}^z}} \over {{{[0.2]}^x}{{[0.1]}^y}{{[0.2]}^z}}} = {{6 \times {{10}^{ - 5}}} \over {1.2 \times {{10}^{ - 4}}}}$$
$$ \Rightarrow $$ z = 1
$${{{{(Rate)}_1}} \over {{{(Rate)}_4}}} = {{{{[0.2]}^x}{{[0.1]}^y}{{[0.1]}^z}} \over {{{[0.3]}^x}{{[0.1]}^y}{{[0.1]}^z}}} = {{6 \times {{10}^{ - 5}}} \over {9 \times {{10}^{ - 5}}}}$$
$$ \Rightarrow $$ x = 1
So, rate = k[A]1[C]1
From exp-Ist,
Rate = $$6.0 \times {10^{ - 5}}$$ mol dm$$ - $$3 s$$ - $$1
6.0 $$ \times $$ 10$$ - $$5 = k[0.2]1[0.1]1
k = 3 $$ \times $$ 10$$ - $$3
Given, [A] = 0.15 mol dm$$ - $$3
[B] = 0.25 mol dm$$ - $$3
[C] = 0.15 mol dm$$ - $$3
$$ \therefore $$ Rate = (3 $$ \times $$ 10$$ - $$3) $$ \times $$ [0.15]1[0.25]0[0.15]1
= 3 $$ \times $$ 10$$ - $$3 $$ \times $$ 0.15 $$ \times $$ 0.15
Rate = 6.75 $$ \times $$ 10$$ - $$5 mol dm$$ - $$3 s$$ - $$1
Thus, Y = 6.75
Comments (0)


