JEE Advance - Chemistry (2018 - Paper 2 Offline - No. 2)
For a reaction, $$A\,\,\rightleftharpoons\,\,P,$$ the plots of $$\left[ A \right]$$ and $$\left[ P \right]$$ with time at temperature $${T_1}$$ and $${T_2}$$ are given below.
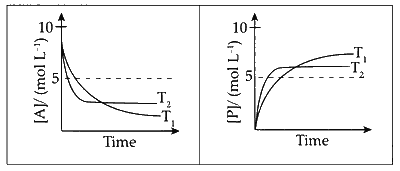
If $${T_2} > {T_1},$$ the correct statement(s) is (are) (Assume $$\Delta {H^ \circ }$$ and $$\Delta {S^ \circ }$$ are independent of temperature and ratio of $$lnK$$ at $${T_1}$$ to $$lnK$$ at $${T_2}$$ is greater than $${{{T_2}} \over {{T_1}}}.$$ Here $$H,$$ $$S,G$$ and $$K$$ are enthalpy, entropy, Gibbs energy and equilibrium constant, respectively.)

If $${T_2} > {T_1},$$ the correct statement(s) is (are) (Assume $$\Delta {H^ \circ }$$ and $$\Delta {S^ \circ }$$ are independent of temperature and ratio of $$lnK$$ at $${T_1}$$ to $$lnK$$ at $${T_2}$$ is greater than $${{{T_2}} \over {{T_1}}}.$$ Here $$H,$$ $$S,G$$ and $$K$$ are enthalpy, entropy, Gibbs energy and equilibrium constant, respectively.)
$$\Delta {H^ \circ } < 0,\Delta {S^ \circ } < O$$
$$\Delta {G^ \circ } < 0,\Delta {H^ \circ } > 0$$
$$\Delta {G^ \circ } < 0,\Delta {S^ \circ } < 0$$
$$\Delta {G^ \circ } < 0,\Delta {S^ \circ } > 0$$
Explanation
For the reaction at equilibrium
$$ \mathrm{A} \rightleftharpoons \mathrm{P} $$
At any temperature:
Concentration of $A$ at equilibrium $[A]_{e q}<5$ Concentration of $\mathrm{B}$ at equilibrium $[\mathrm{P}]_{e q}>5$
Equilibrium constant $\left(\mathrm{K}_{e q}\right)=\frac{[\mathrm{P}]_{e q}}{[\mathrm{~A}]_{e q}}$
$$ \mathrm{K}_{e q}>1 $$
$$ \text{Also,}~~ \frac{\ln \mathrm{K}_{\mathrm{T}_1}}{\ln \mathrm{K}_{\mathrm{T}_2}}>\frac{\mathrm{T}_2}{\mathrm{~T}_1} $$
$$ \begin{aligned} & \text{If}~\mathrm{T}_2 >\mathrm{T}_1 \\\\ & \text{Hence}~\frac{\ln \mathrm{K}_{\mathrm{T}_1}}{\ln \mathrm{K}_{\mathrm{T}_2}} >\frac{\mathrm{T}_2}{\mathrm{~T}_1}>1 \\\\ & \frac{\mathrm{K}_{\mathrm{T}_1}}{\mathrm{~K}_{\mathrm{T}_2}} >1 \\\\ & \mathrm{~K}_{\mathrm{T}_1} >\mathrm{K}_{\mathrm{T}_2} \end{aligned} $$
It can be clearly seen from diagram that concentration of reactant is lesser and that of product is higher at $T_1$ compared to $T_2$. Hence,
equilibrium constant is higher at $\mathrm{T}_1$ than $\mathrm{T}_2$. The reaction is exothermic.
i.e., $\Delta \mathrm{H}^{\circ}<0$ for forward reaction
The expression for the spontaneity and Gibbs free energy of reaction:
$$ \begin{aligned} \Delta \mathrm{G}^{\circ} & =\Delta \mathrm{H}^{\circ}-\mathrm{T} \Delta \mathrm{S}^{\circ} \\\\ \Delta \mathrm{S}^{\circ} & =\frac{\Delta \mathrm{H}^{\circ}-\Delta \mathrm{G}^{\circ}}{\mathrm{T}} \end{aligned} $$
Since, both $\Delta \mathrm{G}^{\circ}$ and $\Delta \mathrm{H}^{\circ}$ are less than zero $\left\{\Delta \mathrm{H}^{\circ}<0\right.$ and $\left.\Delta \mathrm{G}^{\circ}<0\right\}$
If $\Delta \mathrm{H}^{\circ}>\Delta \mathrm{G}^{\circ}$, then $\Delta \mathrm{S}^{\circ}>0$
Otherwise,
If $\Delta \mathrm{H}^{\circ}<\Delta \mathrm{G}^{\circ}$, then $\Delta \mathrm{S}^{\circ}<0$
we know,
$$ \begin{aligned} \Delta \mathrm{G}^{\circ} & =-\mathrm{RT} \ln \mathrm{K} . \\\\ \Delta \mathrm{G}_1^{\circ} & =-\mathrm{RT}_1 \ln \mathrm{K}_{\mathrm{T}_1} \\\\ \text { and } \Delta \mathrm{G}_2^{\circ} & =-\mathrm{RT} \ln \mathrm{K}_{\mathrm{T}_2} \end{aligned} $$
Its given, $\ln \mathrm{K}_{\mathrm{T}_1}>\ln \mathrm{K}_{\mathrm{T}_2}$
$$ \begin{gathered} \Delta \mathrm{G}_1^{\circ}<\Delta \mathrm{G}_2^{\circ} \\\\ \Delta \mathrm{H}_{\mathrm{T}_1}^{\circ}-\mathrm{T} \Delta \mathrm{S}_{\mathrm{T}_1}^{\mathrm{o}}<\Delta \mathrm{H}_{\mathrm{T}_2}^{\mathrm{o}}-\mathrm{T} \Delta \mathrm{S}_{\mathrm{T}_2}^{\mathrm{o}} \end{gathered} $$
This is possible only if $\Delta S^{\circ}<0$
Hence,
$$ \begin{array}{r} \Delta \mathrm{G}^{\circ}<0, \Delta \mathrm{S}^{\circ}<0 \\\\ \Delta \mathrm{H}^{\circ}<0, \Delta \mathrm{S}^{\circ}<0 \end{array} $$
$$ \mathrm{A} \rightleftharpoons \mathrm{P} $$
At any temperature:
Concentration of $A$ at equilibrium $[A]_{e q}<5$ Concentration of $\mathrm{B}$ at equilibrium $[\mathrm{P}]_{e q}>5$
Equilibrium constant $\left(\mathrm{K}_{e q}\right)=\frac{[\mathrm{P}]_{e q}}{[\mathrm{~A}]_{e q}}$
$$ \mathrm{K}_{e q}>1 $$
$$ \text{Also,}~~ \frac{\ln \mathrm{K}_{\mathrm{T}_1}}{\ln \mathrm{K}_{\mathrm{T}_2}}>\frac{\mathrm{T}_2}{\mathrm{~T}_1} $$
$$ \begin{aligned} & \text{If}~\mathrm{T}_2 >\mathrm{T}_1 \\\\ & \text{Hence}~\frac{\ln \mathrm{K}_{\mathrm{T}_1}}{\ln \mathrm{K}_{\mathrm{T}_2}} >\frac{\mathrm{T}_2}{\mathrm{~T}_1}>1 \\\\ & \frac{\mathrm{K}_{\mathrm{T}_1}}{\mathrm{~K}_{\mathrm{T}_2}} >1 \\\\ & \mathrm{~K}_{\mathrm{T}_1} >\mathrm{K}_{\mathrm{T}_2} \end{aligned} $$
It can be clearly seen from diagram that concentration of reactant is lesser and that of product is higher at $T_1$ compared to $T_2$. Hence,
equilibrium constant is higher at $\mathrm{T}_1$ than $\mathrm{T}_2$. The reaction is exothermic.
i.e., $\Delta \mathrm{H}^{\circ}<0$ for forward reaction
The expression for the spontaneity and Gibbs free energy of reaction:
$$ \begin{aligned} \Delta \mathrm{G}^{\circ} & =\Delta \mathrm{H}^{\circ}-\mathrm{T} \Delta \mathrm{S}^{\circ} \\\\ \Delta \mathrm{S}^{\circ} & =\frac{\Delta \mathrm{H}^{\circ}-\Delta \mathrm{G}^{\circ}}{\mathrm{T}} \end{aligned} $$
Since, both $\Delta \mathrm{G}^{\circ}$ and $\Delta \mathrm{H}^{\circ}$ are less than zero $\left\{\Delta \mathrm{H}^{\circ}<0\right.$ and $\left.\Delta \mathrm{G}^{\circ}<0\right\}$
If $\Delta \mathrm{H}^{\circ}>\Delta \mathrm{G}^{\circ}$, then $\Delta \mathrm{S}^{\circ}>0$
Otherwise,
If $\Delta \mathrm{H}^{\circ}<\Delta \mathrm{G}^{\circ}$, then $\Delta \mathrm{S}^{\circ}<0$
we know,
$$ \begin{aligned} \Delta \mathrm{G}^{\circ} & =-\mathrm{RT} \ln \mathrm{K} . \\\\ \Delta \mathrm{G}_1^{\circ} & =-\mathrm{RT}_1 \ln \mathrm{K}_{\mathrm{T}_1} \\\\ \text { and } \Delta \mathrm{G}_2^{\circ} & =-\mathrm{RT} \ln \mathrm{K}_{\mathrm{T}_2} \end{aligned} $$
Its given, $\ln \mathrm{K}_{\mathrm{T}_1}>\ln \mathrm{K}_{\mathrm{T}_2}$
$$ \begin{gathered} \Delta \mathrm{G}_1^{\circ}<\Delta \mathrm{G}_2^{\circ} \\\\ \Delta \mathrm{H}_{\mathrm{T}_1}^{\circ}-\mathrm{T} \Delta \mathrm{S}_{\mathrm{T}_1}^{\mathrm{o}}<\Delta \mathrm{H}_{\mathrm{T}_2}^{\mathrm{o}}-\mathrm{T} \Delta \mathrm{S}_{\mathrm{T}_2}^{\mathrm{o}} \end{gathered} $$
This is possible only if $\Delta S^{\circ}<0$
Hence,
$$ \begin{array}{r} \Delta \mathrm{G}^{\circ}<0, \Delta \mathrm{S}^{\circ}<0 \\\\ \Delta \mathrm{H}^{\circ}<0, \Delta \mathrm{S}^{\circ}<0 \end{array} $$
Comments (0)


