JEE Advance - Chemistry (2018 - Paper 2 Offline - No. 10)
For a first order reaction $$A\left( g \right) \to 2B\left( g \right) + C\left( g \right)$$ at constant volume and $$300K,$$ the total pressure at the beginning $$(t=0)$$ and at time $$t$$ are $${P_0}$$ and $${P_1},$$ respectively. Initially, only $$A$$ is present with concentration $${\left[ A \right]_0},$$ and $${t_{1/3}}$$ is the time required for the partial pressure of $$A$$ to reach $$1/{3^{rd}}$$ of its initial value. The correct option(s) is (are) (Assume that all these gases behave as ideal gases)
Explanation
Total pressure of gaseous mixture at beginning $(T=0)=\mathrm{P}_0$
Total pressure of gaseous mixture after time $t$ $(\mathrm{T}=t)=\mathrm{P}_t$
Initial concentration of $A=[A]_0$
Temperature of the reaction mixture (T) $=300 \mathrm{~K}$
For the first order reaction,
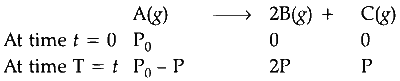
Total pressure after time $(\mathrm{T}=t)=\mathrm{P}_0-\mathrm{P}+2 \mathrm{P} +\mathrm{P}$
$$ \begin{aligned} \mathrm{P}_t=\mathrm{P}_0+2 \mathrm{P} \\\\ \mathrm{P} =\frac{\mathrm{P}_t-\mathrm{P}_0}{2} \end{aligned} $$
According to integrated rate law for the first order reaction:
$$ \begin{aligned} &t =\frac{2.303}{k} \log \frac{\mathrm{P}_0}{\mathrm{P}_t} ~~~~...(i)\\\\ &t =\frac{2.303}{k} \log \frac{\mathrm{P}_0}{\mathrm{P}_0-\mathrm{P}} \\\\ &t =\frac{2.303}{k} \log \frac{\mathrm{P}_0}{\mathrm{P}_0-\frac{\left(\mathrm{P}_t-\mathrm{P}_0\right)}{2}} \\\\ &t =\frac{2.303}{k} \log \frac{2 \mathrm{P}_0}{2 \mathrm{P}_0-\mathrm{P}_t+\mathrm{P}_0} \\\\ &t =\frac{2.303}{k} \log \frac{2 \mathrm{P}_0}{3 \mathrm{P}_0-\mathrm{P}_t} \\\\ &t =\frac{1}{k} \ln \frac{2 \mathrm{P}_0}{3 \mathrm{P}_0-\mathrm{P}_t} \\\\ &\ln \left(3 \mathrm{P}_0-\mathrm{P}_t\right) =\ln \left(2 \mathrm{P}_0-\mathrm{P}_t\right)-k t ~~~~...(ii) \end{aligned} $$
Comparing equation (ii) with equation of straight option line
$$ \begin{aligned} & \ln \left(3 \mathrm{P}_0-\mathrm{P}_t\right) =\ln 2 \mathrm{P}_0-k t \\\\ &y =c+m x \end{aligned} $$
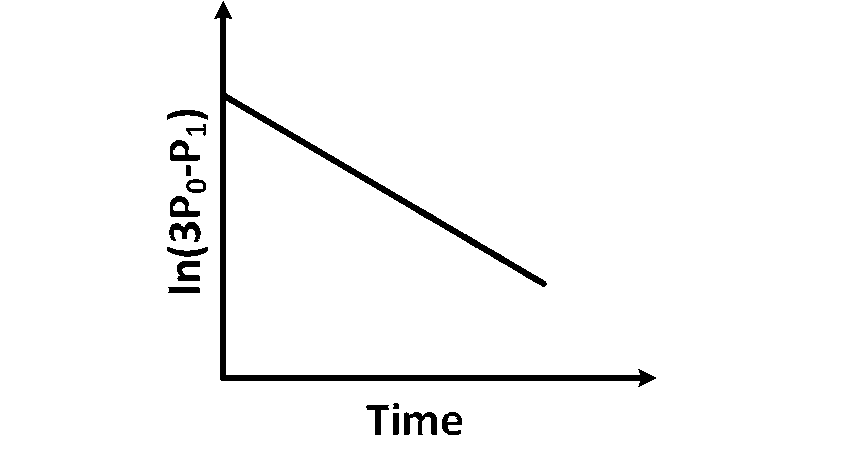
Plot of $\ln \left(3 \mathrm{P}_0-\mathrm{P}_t\right)$ verses time $(t)$ is represented as:
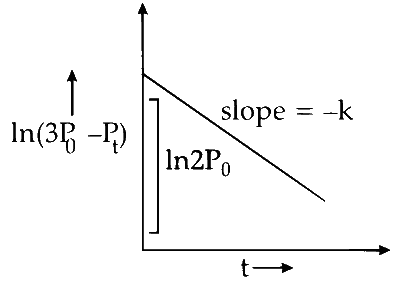
Option (A) is correct.
(ii) For the first order reaction,
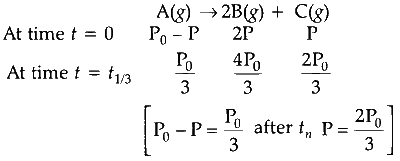
$$ \mathrm{P}_t=\frac{\mathrm{P}_0}{3}+\frac{4 \mathrm{P}_0}{3}+\frac{2 \mathrm{P}_0}{3}=\frac{7 \mathrm{P}_0}{3} $$
Substituting the value of $P_t$ in $e q$ (i)
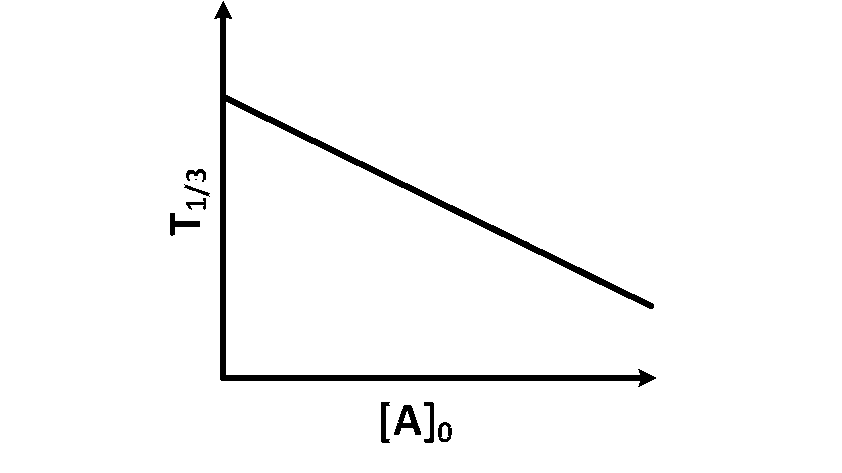
$$ \begin{aligned} t_{1 / 3} & =\frac{2.303}{k} \log \frac{\mathrm{P}_0}{\frac{7 \mathrm{P}_0}{3}} \\\\ t_{1 / 3} & =\frac{2.303}{k} \log \frac{3}{7} \end{aligned} $$
$\mathrm{P}_{t_3}$ is independent of concentration of (A).
Option (B) is not correct.
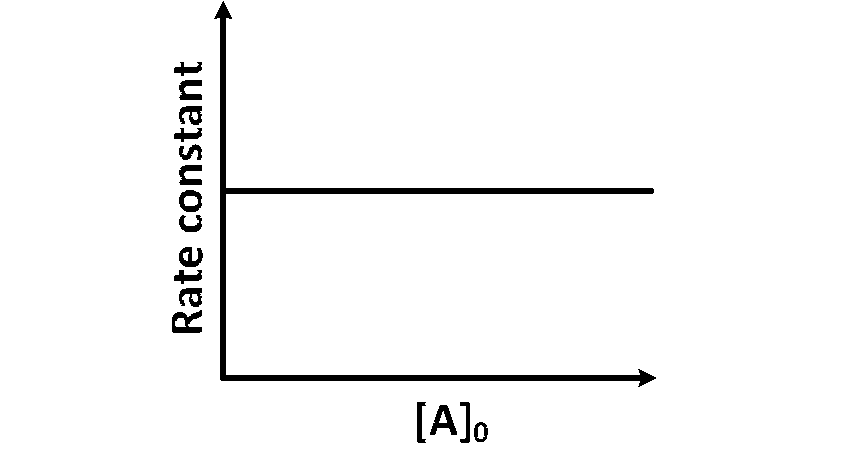
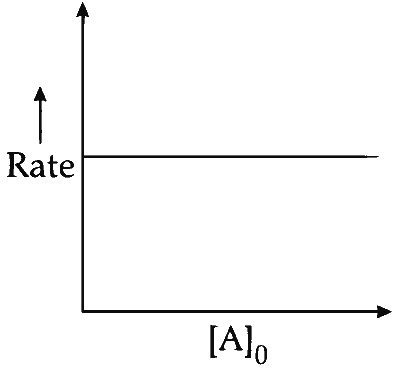
(iii) At any time $t$, rate constant $(k)$ is independent of concentration of [A].
For example:
At $t_{y_3}$ :
$$ k=\frac{2.303}{t_{1 / 3}} \times \log \frac{3}{7} $$
Hence, Option (D) is correct.
Total pressure of gaseous mixture after time $t$ $(\mathrm{T}=t)=\mathrm{P}_t$
Initial concentration of $A=[A]_0$
Temperature of the reaction mixture (T) $=300 \mathrm{~K}$
For the first order reaction,
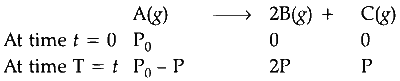
Total pressure after time $(\mathrm{T}=t)=\mathrm{P}_0-\mathrm{P}+2 \mathrm{P} +\mathrm{P}$
$$ \begin{aligned} \mathrm{P}_t=\mathrm{P}_0+2 \mathrm{P} \\\\ \mathrm{P} =\frac{\mathrm{P}_t-\mathrm{P}_0}{2} \end{aligned} $$
According to integrated rate law for the first order reaction:
$$ \begin{aligned} &t =\frac{2.303}{k} \log \frac{\mathrm{P}_0}{\mathrm{P}_t} ~~~~...(i)\\\\ &t =\frac{2.303}{k} \log \frac{\mathrm{P}_0}{\mathrm{P}_0-\mathrm{P}} \\\\ &t =\frac{2.303}{k} \log \frac{\mathrm{P}_0}{\mathrm{P}_0-\frac{\left(\mathrm{P}_t-\mathrm{P}_0\right)}{2}} \\\\ &t =\frac{2.303}{k} \log \frac{2 \mathrm{P}_0}{2 \mathrm{P}_0-\mathrm{P}_t+\mathrm{P}_0} \\\\ &t =\frac{2.303}{k} \log \frac{2 \mathrm{P}_0}{3 \mathrm{P}_0-\mathrm{P}_t} \\\\ &t =\frac{1}{k} \ln \frac{2 \mathrm{P}_0}{3 \mathrm{P}_0-\mathrm{P}_t} \\\\ &\ln \left(3 \mathrm{P}_0-\mathrm{P}_t\right) =\ln \left(2 \mathrm{P}_0-\mathrm{P}_t\right)-k t ~~~~...(ii) \end{aligned} $$
Comparing equation (ii) with equation of straight option line
$$ \begin{aligned} & \ln \left(3 \mathrm{P}_0-\mathrm{P}_t\right) =\ln 2 \mathrm{P}_0-k t \\\\ &y =c+m x \end{aligned} $$
Plot of $\ln \left(3 \mathrm{P}_0-\mathrm{P}_t\right)$ verses time $(t)$ is represented as:

Option (A) is correct.
(ii) For the first order reaction,
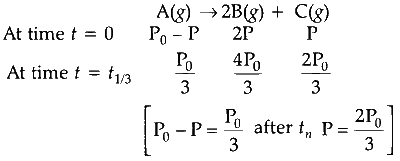
$$ \mathrm{P}_t=\frac{\mathrm{P}_0}{3}+\frac{4 \mathrm{P}_0}{3}+\frac{2 \mathrm{P}_0}{3}=\frac{7 \mathrm{P}_0}{3} $$
Substituting the value of $P_t$ in $e q$ (i)
$$ \begin{aligned} t_{1 / 3} & =\frac{2.303}{k} \log \frac{\mathrm{P}_0}{\frac{7 \mathrm{P}_0}{3}} \\\\ t_{1 / 3} & =\frac{2.303}{k} \log \frac{3}{7} \end{aligned} $$
$\mathrm{P}_{t_3}$ is independent of concentration of (A).
Option (B) is not correct.
(iii) At any time $t$, rate constant $(k)$ is independent of concentration of [A].
For example:
At $t_{y_3}$ :
$$ k=\frac{2.303}{t_{1 / 3}} \times \log \frac{3}{7} $$
Hence, Option (D) is correct.

Comments (0)


