JEE Advance - Chemistry (2018 - Paper 1 Offline - No. 5)
$$(i)\,\,\,\,\,$$ Remove all the anions $$(X)$$ except the central one
$$(ii)\,\,\,\,$$ Replace all the face centered cations $$(M)$$ by anions $$(X)$$
$$(iii)\,\,$$ Remove all the corner cations $$(M)$$
$$(iv)\,\,\,\,$$ Replace the central anion $$(X)$$ with cation $$(M)$$
The value of $$\,\,\left( {{{number\,\,of\,\,anions} \over {number\,\,of\,\,cations}}} \right)\,\,$$ in $$Z$$ is ___________.
Explanation
The unit cell of initial structure of ionic solid MX looks like
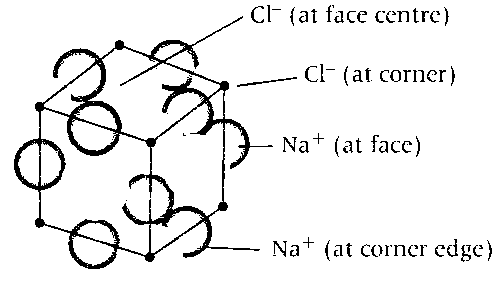
In NaCl type of solids cations (Na+) occupy the octahedral voids while anions (Cl$$-$$) occupy the face centre positions.
However, as per the demand of problem the position of cations and anions are swapped.
We also know that (for 1 unit cell)
(A) Total number of atoms at FCC = 4
(B) Total number of octahedral voids = 4 (as no. of atoms at FCC = No. of octahedral voids)
Now taking the conditions one by one
(i) If we remove all the anions except the central one than number of left anions.
= 4 $$-$ 3 = 1
(ii) If we replace all the face centred cations by anions than effective number of cations will be = 4 $$-$$ 3 = 1 Likewise effective number of anions will be = 1 + 3 = 4
(iii) If we remove all the corner cations then effective number of cations will be 1 $$-$$ 1 = 0
(iv) If we replace central anion with cation then effective number of cations will be 0 + 1 = 1 Likewise effective number of anions will be 4 $$-$$ 1 = 3
Thus, as the final outcome, total number of cations present in Z after fulfilling all the four sequential instructions = 1 Likewise, total number of anions = 3
Hence, the value of $${{Number\,of\,anions} \over {Number\,of\,cations}} = {3 \over 1} = 3$$
Comments (0)


