JEE Advance - Chemistry (2018 - Paper 1 Offline - No. 15)
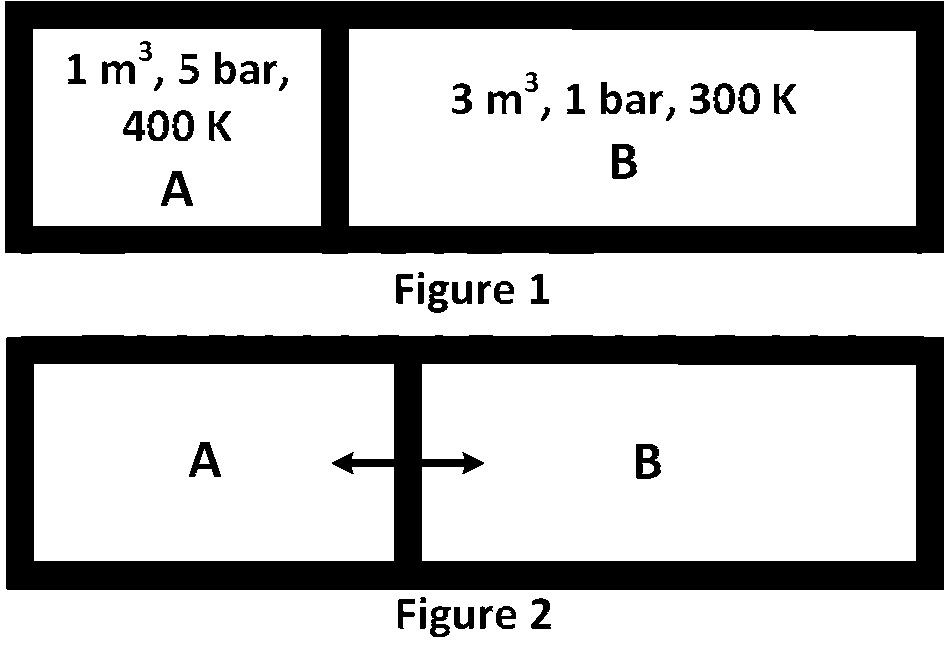
Explanation
Given p1 = 5 bar, V1 = 1 m3, T1 = 400 K
So, $${n_1} = {5 \over {400R}}$$ (from pV = nRT)
Similarly, p2 = 1 bar, V2 = 3 m3, T2 = 300 K,
$${n_2} = {3 \over {300R}}$$
Let at equilibrium the new volume of A will be (1 + x)
So, the new volume of B will be (3 $$-$$ x)
Now, from the ideal gas equation,
$${{{p_1}{V_1}} \over {{n_1}R{T_1}}} = {{{p_2}{V_2}} \over {{n_2}R{T_2}}}$$
and at equilibrium (due to conduction of heat)
$${{{p_1}} \over {{T_1}}} = {{{p_2}} \over {{T_2}}}$$
So, $${{{V_1}} \over {{n_1}}} = {{{V_2}} \over {{n_2}}}$$ or $${V_1}{n_2} = {V_2}{n_1}$$
After putting the values
$$(1 + x) \times {3 \over {300R}} = (3 - x) \times {5 \over {400R}}$$
or $$(1 + x) = {{(3 - x)5} \over 4}$$ or $$4(1 + x) = 15 - 5x$$
or $$4 + 4x = 15 - 5x$$ or $$x = {{11} \over 9}$$
Hence, new volume of A i.e., (1 + x) will comes as $$1 + {{11} \over 9} = {{20} \over 9}$$ or 2.22.
Comments (0)


