JEE Advance - Chemistry (2017 - Paper 1 Offline - No. 4)
An ideal gas is expanded from $$\left( {{p_1},{V_1},{T_1}} \right)$$ to $$\left( {{p_2},{V_2},{T_2}} \right)$$ under different conditions. The correct statement(s) among the following is (are)
The work done on the gas is maximum when it is compressed irreversibly from $$\left( {{p_2},{V_2}} \right)$$ to $$\left( {{p_1},{V_1}} \right)$$ against constant pressure $${p_1}$$
If the expansion is carried out freely, it is simultaneously both isothermal as well as adiabatic
The work done by the gas is less when it is expanded reversibly from $${V_1}$$ to $${V_2}$$ under adiabatic conditions as compared to that when expanded reverseibly from $${V_1}$$ to $${V_2}$$ under isothermal conditions
The change in internal energy of the gas is (i) zero, if it is expanded reversibly with $${T_1} = {T_2}$$ , and (ii) positive, if it is expanded reversibly under adiabatic conditions with $${T_1}\, \ne \,{T_2}$$
Explanation
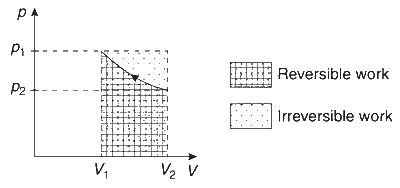
Option (A): Correct. For compression of gas, $V_2 < V_1$, thus, from $w=-p \Delta V$, work done on the gas will be positive. Below graph shows the pressure-volume curve for work done during reversible and irreversible compression process. Area under curve during irreversible process is greater than the area under curve during reversible process. Therefore, work done on the gas in irreversible process is greater than in reversible process, that is, $w_{\text {irr }}>w_{\text {rev }}$.
Option (B): Correct. For work done in free expansion, $p_{\text {ext }}=0$, therefore, $w=0$. For an adiabatic process, $q=0$ and for isothermal process, $\Delta T=0$. Therefore, from first law of thermodynamics, $\Delta U=q+w=0$.
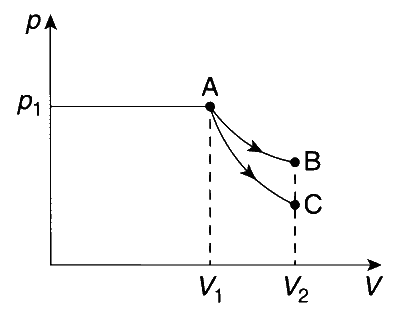
Option (C): Correct. Below graph represents the expansion under adiabatic (AC) and isothermal condition (AB). Therefore, $\left|w_{\mathrm{AB}}\right|>\left|w_{\mathrm{AC}}\right|$.

Option (B): Correct. For work done in free expansion, $p_{\text {ext }}=0$, therefore, $w=0$. For an adiabatic process, $q=0$ and for isothermal process, $\Delta T=0$. Therefore, from first law of thermodynamics, $\Delta U=q+w=0$.
Option (C): Correct. Below graph represents the expansion under adiabatic (AC) and isothermal condition (AB). Therefore, $\left|w_{\mathrm{AB}}\right|>\left|w_{\mathrm{AC}}\right|$.

Comments (0)


